Paillier算法

介绍

1999年欧密会上，首次提出Paillier算法，2001年，Damgard等人对该方案简化，推出当前最优的Paillier方案。

加密方案

Carmichael函数

困难问题

合数剩余类问题(Composite Residuosity Class Problem)

该算法基于复合剩余类的困难问题

判定合数剩余假设问题（DCRA）也可以描述为：给定一个合数n和整数z，判定z在n²下n次剩余是否困难。

n次剩余：若存在一个整数y，使得yⁿ=z mod n² 成立，则z是n²的一个n次剩余。

判断整数z是否为n²的n次剩余问题，不存在多项式时间的解法，且该问题对于任意的n难度都是一样的。

加解密

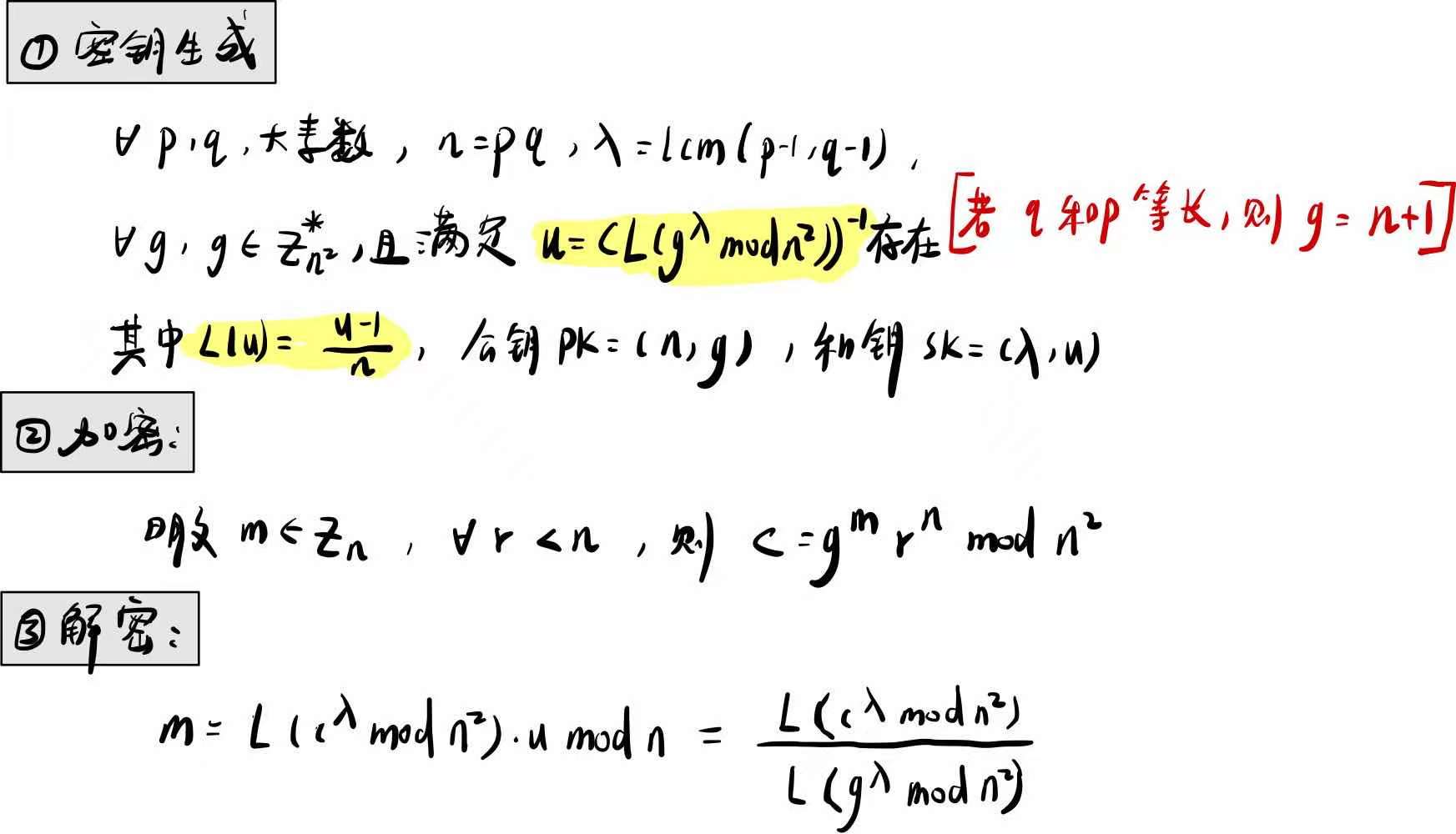
正确性

费马小定理：

若p是一个素数，a不是p的倍数，则a^p-1=1 mod p。

这里g^p-1 = 1mod p，即(g^p-1)^k= 1mod p。

同态性

Paillier具有加法同态性和一次乘法同态性

疑问

为什么只能具有一次乘法同态性 ？

参考

1、Paillier Cryptosystem

2、Paillier  同态密码在隐私保护中的应用研究-魏文燕

3、Paillier解密正确性[Paillier密码体制]

4、Carmichael function[卡迈克尔函数相关性质]