UVA10294 Arif in Dhaka (First Love Part 2) —— 置换、poyla定理

题目链接：https://vjudge.net/problem/UVA-10294

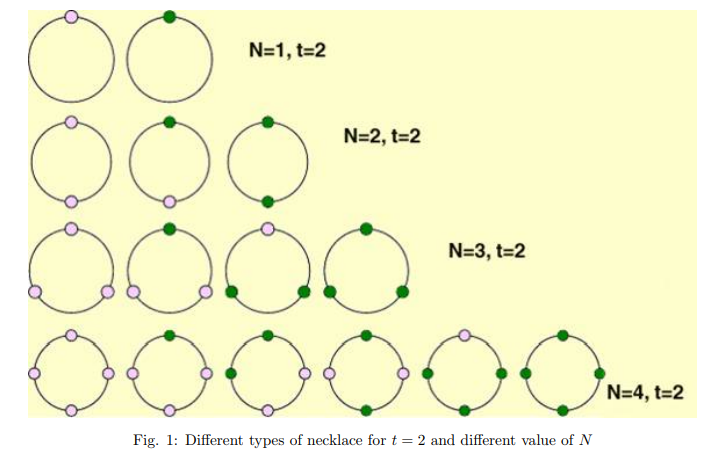
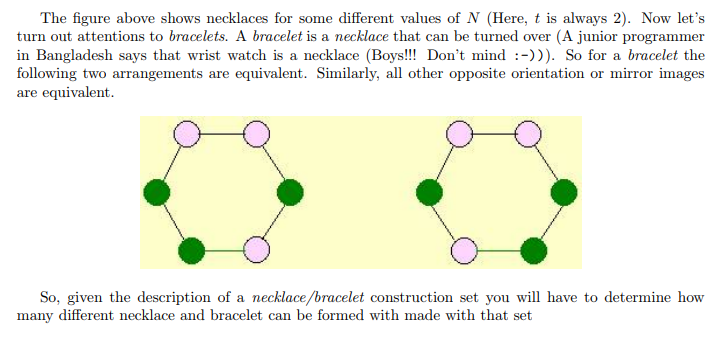
题解：

白书P146~147。

为什么旋转i个间距，就有gcd(i,n)个循环，且每个循环有n/gcd(i,n)个元素？

证明：

　　(gcd:最大公约数，lcm:最小公倍数)

将珠子从0到n-1标号，对于旋转i位的置换，在以0号为起点，长度为t的一个循环节中，元素标号为：0,i%n,(i*2)%n,…,(i*(t-1))%n

易知：(i*t)%n==0（循环大小为t，跳t次就回到初始点0），即 n*k == i*t，其中n,k,i,t为正整数，因此等式左右的最小值为lcm(n,i)，即i*t==lcm(n,i)，为什么i*t取最小值，即t取最小值？因为是从0第一次跳到0就完成整个循环的遍历，这个“第一次”就决定了是最早满足条件的那个t，即最小t。

∴ t == lcm(n,i)/i == ( n*i/gcd(n,i) )/i == n/gcd(n,i)

∴ 循环节t==n/gcd(n,i)，循环节的个数为：n/t == gcd(n,i)

代码如下：

 #include <iostream>
 #include <cstdio>
 #include <cstring>
 #include <algorithm>
 #include <vector>
 #include <cmath>
 #include <queue>
 #include <stack>
 #include <map>
 #include <string>
 #include <set>
 using namespace std;
 typedef long long LL;
 const int INF = 2e9;
 const LL LNF = 9e18;
 const int MOD = 1e9+;
 const int MAXN = ;

 LL gcd(LL a, LL b)
 {
     return b==?a:gcd(b,a%b);
 }

 LL Pow[MAXN];
 int main()
 {
     int n, t;
     while(scanf("%d%d", &n,&t)!=EOF)
     {
         Pow[] = ;
         for(int i = ; i<=n; i++) Pow[i] = 1LL*Pow[i-]*t;
         LL a = , b = ;
         for(int i = ; i<n; i++)
             a += Pow[gcd(i,n)];
         if(n%)
             b = 1LL*n*Pow[n/+];
         else
             b = 1LL*n/*(Pow[n/]+Pow[n/+]);

         printf("%lld %lld\n", a/n, (a+b)//n);
     }
 }