2017 ACM/ICPC Asia Regional Shenyang Online cable cable cable

Problem Description

Connecting the display screen and signal sources which produce different color signals by cables, then the display screen can show the color of the signal source.Notice that every signal source can only send signals to one display screen each time. 
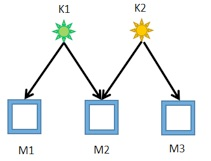
Now you have M display screens and K different signal sources(K≤M≤2³²−1). Select K display screens from M display screens, how many cables are needed at least so that **any** K display screens you select can show exactly K different colors.

Input

Multiple cases (no more than 100), for each test case:
there is one line contains two integers M and K.

Output

Output the minimum number of cables N.

Sample Input

3 2

20 15

 

Sample Output

4

90

没什么要说的

 #include <bits/stdc++.h>
 using namespace std;
 int main(){
     long long n,m;
     while(cin>>n>>m){
         if(n<=m){
             cout<<n<<endl;
         }else{
             cout<<(n-m+)*m<<endl;
         }
     }
     return ;
 }