Huber鲁棒损失函数

在统计学习角度，Huber损失函数是一种使用鲁棒性回归的损失函数，它相比均方误差来说，它对异常值不敏感。常常被用于分类问题上。

下面先给出Huber函数的定义：

这个函数对于小的a值误差函数是二次的，而对大的值误差函数是线性的。变量a表述residuals，用以描述观察值与预测值之差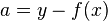：，因此我们可以将上面的表达式写成下面的形式：

Huber loss (green, 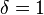) and squared error loss (blue) as a function of 

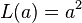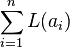两个最常用的损失函数是平方损失（L2），，和绝对值损失（L1）。然而绝对损失在特定点上不可微分，a=0，在a=0点上对它等于区间[-1,+1]的凸次微分是可微分的；绝对值损失函数导致了中值无偏的估计器，它可以通过线性编程为特定的数据集评估。平方损失有着它的缺点：它倾向于对异常值敏感--当累加一组a(as in  )时,当数据时重尾分布是（根据估计理论，中值的渐进相关效率会在重尾分布时表现的较差）采样均值会受少量的较大的值的影响。

像上面定义的那样，在Huber损失函数的最小值在a=0周边邻域上是凸的，huber损失函数将拓展了 和 上的微分到仿射函数上。这些特性允许结合均值无偏的敏感性、均值的最小变化估计器（二次损失函数）和无偏中值估计器的鲁棒性（绝对值损失函数）。

伪Huber损失函数

伪Huber损失函数是Huber函数的平滑版本，而且确保了所有角度上是连续可导的。它可以被定义成：

像上面公式描述的那样，对于小的值a，这个损失函数的值可以表示为a/2，对于较大的a值可以近似成一条斜率为 的直线。当然也存在其他形式的伪Huber损失函数。

分类问题上的演变

对于分类问题，一种Huber损失函数的变形--modified Huber常常被使用。给定一个预测函数f（x）和一个真实的二元分类标签，modified Huber可以被定义为：

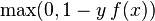项就是只用在SVM上的hinge loss，二次平滑的hinge loss就是L的通用表达形式。

应用

Huber 损失函数常常用于鲁棒性系统分析，M元估计和适应性建模。