POJ 1470 Closest Common Ancestors（最近公共祖先 LCA）

POJ 1470 Closest Common Ancestors（最近公共祖先 LCA）

Description

Write a program that takes as input a rooted tree and a list of pairs of vertices. For each pair (u,v) the program determines the closest common ancestor of u and v in the tree. The closest common ancestor of two nodes u and v is the node w that is an ancestor of both u and v and has the greatest depth in the tree. A node can be its own ancestor (for example in Figure 1 the ancestors of node 2 are 2 and 5)

Input

The data set, which is read from a the std input, starts with the tree description, in the form:

nr_of_vertices

vertex:(nr_of_successors) successor1 successor2 ... successorn

...

where vertices are represented as integers from 1 to n ( n <= 900 ). The tree description is followed by a list of pairs of vertices, in the form:

nr_of_pairs

(u v) (x y) ...

The input file contents several data sets (at least one).

Note that white-spaces (tabs, spaces and line breaks) can be used freely in the input.

Output

For each common ancestor the program prints the ancestor and the number of pair for which it is an ancestor. The results are printed on the standard output on separate lines, in to the ascending order of the vertices, in the format: ancestor:times

For example, for the following tree:

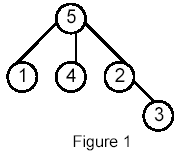
Sample Input

5

5:(3) 1 4 2

1:(0)

4:(0)

2:(1) 3

3:(0)

6

(1 5) (1 4) (4 2)

(2 3)

(1 3) (4 3)

Sample Output

2:1

5:5

Http

POJ:https://vjudge.net/problem/POJ-1470

Source

最近公共祖先LCA

题目大意

给出一棵树，统计若干组对最近公共祖先的询问，输出每个点被统计为最近公共祖先多少次

解决思路

这个题就是多次统计LCA，笔者在这里采用在线倍增的方法，具体操作可以看笔者之前的文章

这个题最恶心的地方就是输入了

代码

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
#include<vector>
using namespace std;

const int maxN=901;
const int inf=2147483647;

int n;
int root;
vector<int> E[maxN];
int Parent[maxN][20];
int Depth[maxN];
int Cnt[maxN];
bool vis[maxN];

void LCA_init();
void dfs(int u);
int LCA(int a,int b);

int main()
{
    while (cin>>n)
    {
        for (int i=1;i<=n;i++)
            E[i].clear();
        memset(Parent,0,sizeof(Parent));
        memset(Depth,0,sizeof(Depth));
        memset(Cnt,0,sizeof(Cnt));
        memset(vis,0,sizeof(vis));
        for (int i=1;i<=n;i++)//-------输入开始-------
        {
            int u,nn;
            scanf("%d:(%d)",&u,&nn);
            for (int j=1;j<=nn;j++)
            {
                int v;
                scanf("%d",&v);
                E[u].push_back(v);
                vis[v]=1;
            }
        }
        for (int i=1;i<=n;i++)
            if (vis[i]==0)
            {
                root=i;
                break;
            }
        LCA_init();
        int Q;
        scanf("%d",&Q);
        for (int i=1;i<=Q;i++)
        {
            int u,v;
            scanf(" (%d %d)",&u,&v);
            //cout<<LCA(u,v)<<endl;
            Cnt[LCA(u,v)]++;
        }//-------输入结束-------
        for (int i=1;i<=n;i++)
            if (Cnt[i]!=0)
                printf("%d:%d\n",i,Cnt[i]);
    }
    return 0;
}

void LCA_init()//LCA初始化
{
    Depth[root]=0;
    dfs(root);
    /*for (int i=1;i<=n;i++)
    {
        for (int j=0;j<=15;j++)
            cout<<Parent[i][j]<<' ';
        cout<<endl;
    }
    cout<<endl;*/
    for (int j=1;j<=15;j++)
        for (int i=1;i<=n;i++)
            Parent[i][j]=Parent[Parent[i][j-1]][j-1];
    /*for (int i=1;i<=n;i++)
    {
        for (int j=0;j<=15;j++)
            cout<<Parent[i][j]<<' ';
        cout<<endl;
    }*/
    return;
}

void dfs(int u)
{
    for (int i=0;i<E[u].size();i++)
    {
        int v=E[u][i];
        Depth[v]=Depth[u]+1;
        Parent[v][0]=u;
        //cout<<"---"<<v<<' '<<Parent[v][0]<<endl;
        dfs(v);
    }
    return;
}

int LCA(int a,int b)//倍增法计算LCA
{
    if (Depth[a]<Depth[b])
        swap(a,b);
    for (int i=15;i>=0;i--)
        if ((Parent[a][i]!=0)&&(Depth[Parent[a][i]]>=Depth[b]))
            a=Parent[a][i];
    if (a==b)
        return a;
    for (int i=15;i>=0;i--)
        if ((Parent[a][i]!=0)&&(Parent[b][i]!=0)&&(Parent[a][i]!=Parent[b][i]))
        {
            a=Parent[a][i];
            b=Parent[b][i];
        }
    return Parent[a][0];
}