51nod 1058 N的阶乘的长度 位数公式

1058 N的阶乘的长度
基准时间限制：1 秒 空间限制：131072 KB 分值: 0 难度：基础题 收藏 关注
输入N求N的阶乘的10进制表示的长度。例如6! = 720，长度为3。
Input
输入N(1 <= N <= 10^6)
Output
输出N的阶乘的长度
Input示例
6
Output示例
3
思路：
位数公式

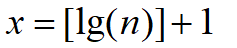
则有:

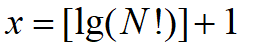
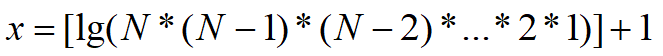
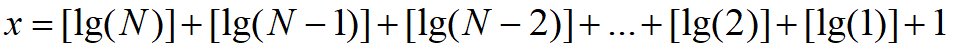
循环遍历即可

代码：

 #include <bits/stdc++.h>
 using namespace std;
 int main() {
     ios::sync_with_stdio(false);
     int N;
     cin>>N;
     double digit=;
     for(int i=;i<=N;++i) {
         digit+=log10(i*1.0);
     }
     cout<<(int)digit+<<endl;
     return ;
 }