Codeforces 888E Maximum Subsequence

原题传送门

E. Maximum Subsequence

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

You are given an array a consisting of n integers, and additionally an integer m. You have to choose some sequence of indices b₁, b₂, ..., b_k (1 ≤ b₁ < b₂ < ... < b_k ≤ n) in such a way that the value of 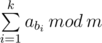is maximized. Chosen sequence can be empty.

Print the maximum possible value of .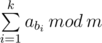

Input

The first line contains two integers n and m (1 ≤ n ≤ 35, 1 ≤ m ≤ 10⁹).

The second line contains n integers a₁, a₂, ..., a_n (1 ≤ a_i ≤ 10⁹).

Output

Print the maximum possible value of .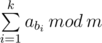

Examples

Input

4 4
5 2 4 1

Output

3

Input

3 20
199 41 299

Output

19

Note

In the first example you can choose a sequence b = {1, 2}, so the sum 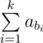is equal to 7 (and that's 3 after taking it modulo 4).

In the second example you can choose a sequence b = {3}.

分析：看到n≤35的条件时确实应该想到什么——假如n≤25，那么直接穷举2ⁿ情况即可，那么这个想法能否应用到35的情况中呢？答案时肯定的：使用Meet-in-the-Middle算法，即将原数组拆成两半，每一半都枚举2n/2个和（当然要mod m了），然后分别排序，枚举左半边取的和，再在右半边二分查找能拼出来的最大的和（假如左半边为x，则对右半边数组lower_bound(c,c+(1<<nr),m-x)-c-1，最后减1的原因是恰好求出小于m-x的最大值，即为答案）。这个算法能够成立的原因是：左右两边是加的关系，因此不存在加起来大于m，并且mod m后比不大于m的情况大——即(x+y)mod m<=max(x,y) mod m (0≤x,y<m)。

实现起来还是很简单的。

代码