寻找图的强连通分量：tarjan算法简单理解

1、简介
tarjan是一种使用深度优先遍历（DFS）来寻找有向图强连通分量的一种算法。

2、知识准备
栈、有向图、强连通分量、DFS。

3、快速理解tarjan算法的运行机制
提到DFS，能想到的是通过栈来储存沿途的点，可以找到所有的环。环本身就是联通的，所以环对于强连通分量来说环已经很接近最终答案了。要把找环变成找强连通管分量还要考虑：
a.在环外是不是有其他环在这个强连通分量内（极大性）

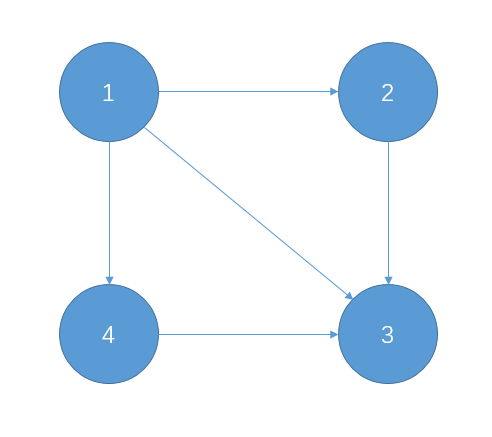
（会被认为是2个环）

b.一些不能构成环的点无法被考虑到，而他们本身就是强连通分量

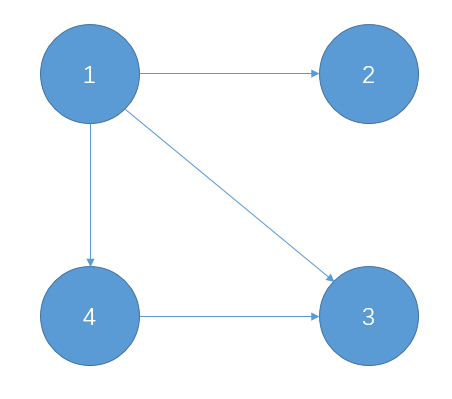
（2不被认为是一个强连通分量）

所以Tarjan算法除了栈还引入了2个数组，分别是：
DFN[N]//节点的时间戳，用来标记节点访问的先后顺序（以及是否被访问过）
Low[N]//当前“环”里最先被访问到的节点，相当于当前这个强连通分量里的根

Tarjan的流程是：
DFS，每遇到一个未被访问过的节点就初始化DFN[i]=Low[i]=index++；
如果找到了环，就在遍历中用Low数组向上传递根的时间戳，直到找到一个点他的时间戳和根的时间戳一致，即DFN[i]=Low[i]，这就说明这个点就是根。此时，栈内的所有在根后面的点（包括根）就组成一个强连通分量。

4、伪代码

index=;
tarjan(u)
{
    DFN[u]=low[u]=index++;
    u入栈;
    for(遍历每条边(u,v))
    {
        if(v未被访问)
        {
            tarjan(v);//DFS
            low[u]=min(low(u),DFN(v));//将下方的时间戳向上传递
        }
        else if(v在栈内)
        {
            low[u]=min(low[u],DFN(v));//找到环，比较当前保存的根的时间戳和v的时间戳，取较早的那个作为根
        }
        if(DFN(u)==low[u])
        {
            //回到了根节点，此时栈内从u往后的节点都是该强连通分量的节点
            //找到了强连通分量，逐个退栈，输出
        }
    }
}

5、进一步说明
a.对于问题a，为什么能找到强连通分量内其他的环？
DFS的问题在于，找到了环立即处理而不考虑其他环；Tarjan算法把输出交给根节点处理，在到根节点之前，算法已经遍历的根节点下的所有节点，自然也把所有环放入了栈。
b.对于问题b，为什么考虑到了不能构成环的那些节点？
对于这些节点，DFN(u)==low[u]，相当于他们本身就是强连通分量的根节点。

6、延伸阅读
如果您仍然有疑问，可以参考https://blog.csdn.net/qq_34374664/article/details/77488976