python多项式求解

1. 例如：p(x) = x³ - 3x+5
   1. 可以使用向量P=[1,0,-3,5]表示，向量长度减一表示多项式最高项次数。
   2. 从右到左分别是变量x的0次幂、1次幂、2次幂……n次幂。
   3. 这里可以使用numpy的方法ployval进行计算。

      1.  import numpy as np
          p = np.array([1,0,-3,5])
          x=5
          print(np.polyval(p,x))
         
          x = [1,2,3,4,5]
          print(np.polyval(p,x))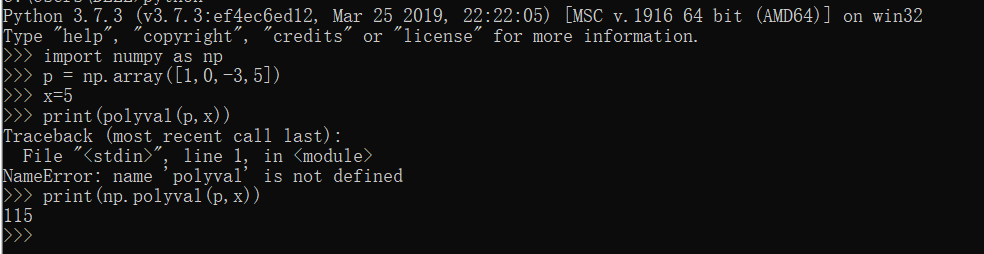

         

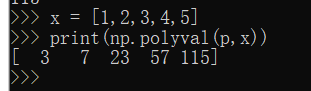
      2. 
2. 上图所示求出X为不同值时多项式的值，同样np内也有方法可以求出多项式的根。

   1. import numpy as np
      
      p = np.array([1,0,-3,5])
      b = np.roots(p)                                     #求根
      
      print(b)
      
      r = np.real(b)                                              #取实数
      
      print(r)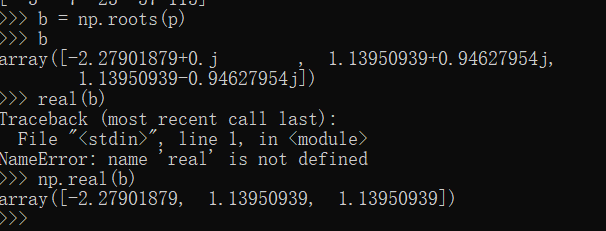

      

3. 多项式乘法
   1. 　　在泛函分析中，卷积（convolution）是通过两个函数 f 和 g 生成第三个函数的一种数学算子，表示函数 f 经过翻转与平移与 g 的重叠部分的累积。
      1. 　

         import numpy as np
         
         a = np.array([1,2,3,4])
         
         b = np.array([1,4,9,16])
         
         print(np.convolve(a,b))

         即(x³+2x²+3x+4 )X (x³+4x²+9x+16)  =  [1,2,20,50,75,84,64]

      2. 

未完待续……