QM4_Probability

　　

Basic Concepts

Probability concepts

Terms

• Random variable
  • A quantity whose possible values are uncertain.
• Outcomes
  • The possible values of a random variable.
• Event
  • A specified set of outcomes.

Properties

• 0 <= P(E) <=1
• 

Events

Odds (赔率)

Odds for the event E

• P(E)/[1-P(E)]

Odds against the event E

• [1-P(E)]/P(E)

Example

• Goven (horse will win the race) = 1/8, what are the odds for or against the horse will win the race?
  • Odds for horse will win the race = (1/8) / (1-1/8) = 1/7
  • Odds against horse will win the race = (1-1/8) / (1/8) = 7/1

Rule

Multplication rule **

• P(A|B) = P(AB)/P(B)
• P(AB) = P(B)xP(A|B) = P(A)xP(B|A)
• For mutually exclusive enents: P(AB) = 0
• For independent events: P(AB) = P(A)P(B)

Addition rule

• P(A+B) = P(A)+P(B)-P(AB)
• For mutually exclusive events: P(A+B) = P(A)+P(B)
• 

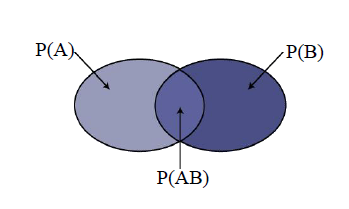
• 含义:
  • P(A|B) : 在B发生的条件下A发生;
  • P(B|A): 在A发生的条件下B发生;
  • P(AB): A发生且B也发生.

Total probability rule (全概率法则)

• 全概率法则, 包含了所有可能发生的情况
• Definition
  • explains the unconditional probability of the event in terms of probabilities conditional on the scenarios.
• Formula
  • P(A) = P(A|S1)P(S1) + P(A|S2)P(S2)... + P(A|Sn)P(Sn)
  • where S1,S2...Sn are mutually exclusive and exhaustive.
  • 其实就是乘法法则 P(A|S1)P(S1) = P(AS1)
  • 

• • 其实就是乘法法则, P(AS1)+P(AS2)+P(AS3)+P(AS1=4)
    • 　　P（AS1）= PS1（PA|S1）

Baye's formula (贝叶斯公式)

• Definition
  • given a prior probabilities P(A) for an event, if you receiv new information (B), the rule for updating your probability(posterior probability, P(A|B)) of the event.
• forula:
• 

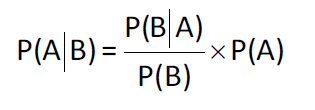
• 例;

  • 

  • 

Probability Statistics

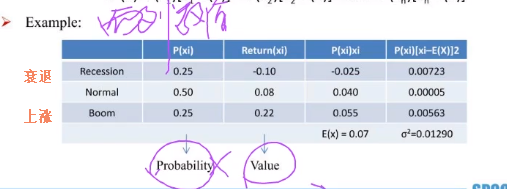
Expected value **

• Definition
  • the probability-weighted average of the possible outcomes of the random variable(X)
• Calculation
  • E(X) = P(X1)X1 + P(X2)X2 ... + P(Xn)Xn
    • • 

        

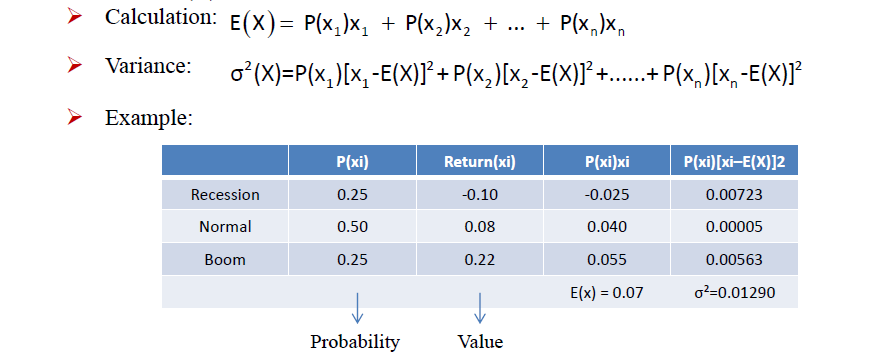
      • E(x)就是x拔, 求方差也就是在求期望. 期望中的权重变成了这里方差中的概率.

• 其实求方差也是在求加权平均
• 算期望就是算加权平均. 相当于基于概率的加权平均. 所以计算期望需要两个值, probability和value.
• 

Covariance (协方差) ***

• Definition
  • A easure of how two variables move together. 两个随机变量变动的方向性.
• Calculation

• 

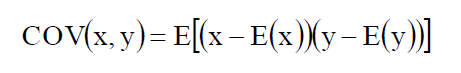
• Characteristics
  • Positive covariance: the two variables tend to move together. 你涨我也涨,你跌我也跌.
  • Negative covariance: the two variables tend to move in apposite direction. 你涨我跌.
  • Valuses range from minus infinity to positive infinity
  • Units of covariance difficult to interpret (比如若是人的平方, 这样的单位没有任何意义)
  • Autocovariance is equal to the variance? 这句话怎么理解?
    • 
      • 协方差是衡量两个变量,所以把(x-x拔)(x-x拔)的其中一个x变成了y.　其实和方差是一样的.　

Correlation (相关系数,相关性) ***

• Definition
  • A standardized measure of linear relationship between two variables.
• Calculation
  • 

    • 分母是标准差, 分子是协方差, 即协方差 / 标准差.

    • 例:
      • 
      • 相关系数 = 协方差 / 标准差, 题目中协方差是0.80, 标准差没有告诉 , 告诉的是variance 0.0036/ 0.0009, 需要开个根号.
      • covariance = correlation * 标准差, 即, covariance = 0.80*0.03*0.06 = 0.00144.

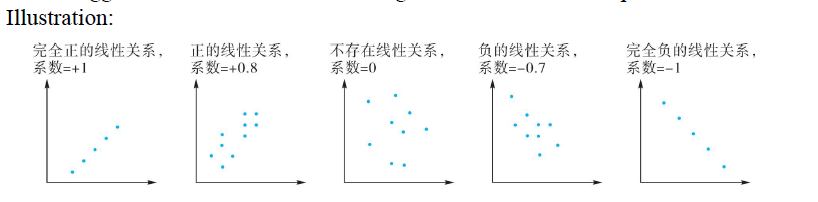
• Characteristics
  • Values range from -1 (perfect negative correlation) to +1 (perfect positive correlation)
  • A correlation of 0 indicates an absence of any linear(straight-line) relationship and doesn't indicate independence (相关系数是0只说明两个变量没有线性关系, 不代表两个变量互不影响. 比如y=x*x,虽然不是线性关系, 但是抛物线)
  • The bigger the absolute value, the stronger the linear relationship.
  •