●洛谷P3233 [HNOI2014]世界树

题链：

https://www.luogu.org/problemnew/show/P3233
题解：

虚树，dp，倍增。

首先对于每个询问，要把虚树建出来，这一步就从略了。这里着重分享一下如何求答案。

比如，我们建出来如下一颗虚树，给出的关键点是那些黑点点们，红点点是"被迫"加入的LCA

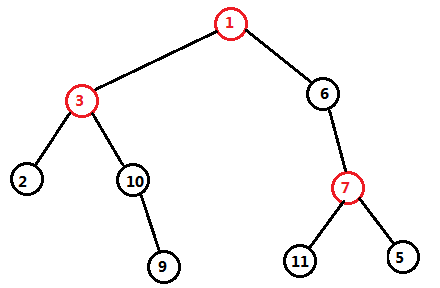
然后，我们就要去求每个黑点的答案了！

等等，YY了一会儿，发现好像现在还并不方便直接求。

那么我们一步一步来，先求出这颗虚树上的每个节点属于哪个黑点管辖(到哪个黑点最近)。

用near[u]表示距离u点最近的黑点是哪个，dis[u]表示u点到near[u]的距离

怎么做呢？

首先，赋一下初值，然后两个dp，就完了。

首先，黑点当然被自己管辖，所以near[u]=u,dis[u]=0

然后进行第一个dp，我们尝试用儿子v去更新其父亲u。

if dis[u]>dis[v]+e[u->v] then near[u]=near[v],dis[u]=dis[v]+e[u->v]

这个e[u->v]就是u到v的距离，在建虚树时得到。

然后进行第二个dp，我们尝试用父亲u去更新儿子v。

if dis[v]>dis[u]+e[u->v] then near[v]=near[u],dis[v]=dis[u]+e[u->v]

这样之后，就得到这颗虚树正确的near[]和dis[]，

换句话说，我们已经知道了原树上的最最最关键的那些点究竟是属于哪个黑点管辖的。

接下来就是看如何处理其它点。

我们先把虚树画再详细一点：

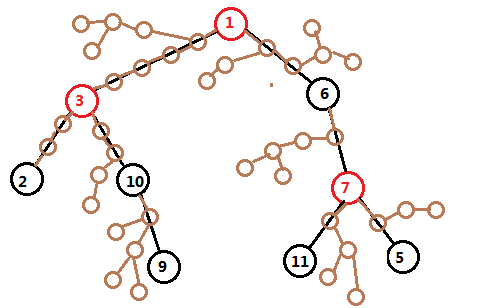
棕色的点就是被虚树省略掉的不重要的点，

而现在我们需要确定的就是这些点会怎样给那些黑点贡献答案。

显然我们不能一个一个地去考虑棕色的点。

但是注意到，所有棕色的节点都是从虚树的边上长出来的，（或者从虚树上的点长出来的），

所以我们的做法是：

1)、依次考虑每条虚树的边：

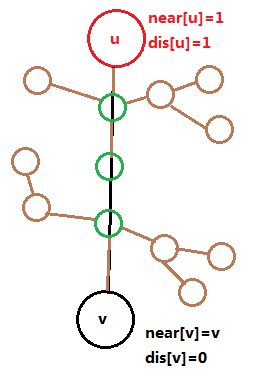
我们把一条虚树的边放大，假设它长这样。

虽然边上长出去的点依旧繁多复杂，但是不难注意到，

我们需要考虑的仅仅是虚树边上的那些绿点到底是属于near[u]，还是near[v]，

而其它的棕色点，只需要跟随其绿点父亲就好啦。

显而易见，在那条绿色的链上，会存在一个分界点，

分界点以上的绿点和棕点，被near[u]管辖，

分界点以下的绿点和棕点，被near[v]管辖：

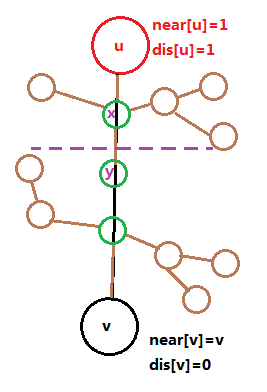
而那个分界点，就直接用倍增去找就好了。

然后用size[]数组的差值去直接贡献给near[u]或near[v]就好了。

2)、其它直接长在虚树点上的棕色点

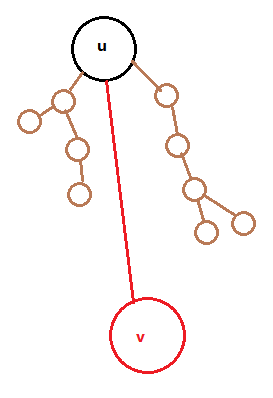
对于这种点，当然直接是从哪个u长出来，就被哪个near[u]所管辖。

也只用size[]的差值就可以计算出他们的贡献。

以上就是所有的情况，在代码实现的时候，还需要三思而后行哦。

代码：

#include<bits/stdc++.h>
#define MAXN 300005
#define INF 0x3f3f3f3f
using namespace std;
int N,Q,M;
bool mark[MAXN];
int fa[MAXN][20],dfn[MAXN],deep[MAXN],size[MAXN];
int near[MAXN],dis[MAXN],ANS[MAXN];
struct Edge{
	int ent;
	int to[MAXN*2],val[MAXN*2],nxt[MAXN*2],head[MAXN];
	Edge(){ent=2;}
	void Adde(int u,int v,int w){
		to[ent]=v; val[ent]=w; nxt[ent]=head[u]; head[u]=ent++;
	}
}E1,E2;
bool cmp(int a,int b){return dfn[a]<dfn[b];}
void read(int &x){
	static int sign; static char ch;
	x=0; sign=1; ch=getchar();
	for(;ch<'0'||'9'<ch;ch=getchar()) if(ch=='-') sign=-1;
	for(;'0'<=ch&&ch<='9';ch=getchar()) x=x*10+ch-'0';
	if(sign==-1) x=-x;
}
void dfs(int u,int dep){
	static int dnt;
	deep[u]=dep; size[u]=1; dfn[u]=++dnt;
	for(int k=1;k<20;k++) fa[u][k]=fa[fa[u][k-1]][k-1];
	for(int e=E1.head[u];e;e=E1.nxt[e]){
		int v=E1.to[e]; if(v==fa[u][0]) continue;
		fa[v][0]=u; dfs(v,dep+1); size[u]+=size[v];
	}
}
int LCA(int u,int v){
	if(deep[u]>deep[v]) swap(u,v);
	for(int k=19;k>=0;k--) if(deep[fa[v][k]]>=deep[u]) v=fa[v][k];
	if(u==v) return u;
	for(int k=19;k>=0;k--) if(fa[u][k]!=fa[v][k]) u=fa[u][k],v=fa[v][k];
	return fa[u][0];
}
void dp1(int u){
	if(mark[u]) near[u]=u,dis[u]=0;
	for(int e=E2.head[u];e;e=E2.nxt[e]){
		int v=E2.to[e]; dp1(v);
		if(dis[u]<dis[v]+E2.val[e]) continue;
		if(dis[u]==dis[v]+E2.val[e]&&near[u]<near[v]) continue;
		near[u]=near[v]; dis[u]=dis[v]+E2.val[e];
	}
}
void dp2(int u){
	for(int e=E2.head[u];e;e=E2.nxt[e]){
		int v=E2.to[e];
		if(dis[v]>dis[u]+E2.val[e]||(dis[v]==dis[u]+E2.val[e]&&near[v]>near[u]))
			near[v]=near[u],dis[v]=dis[u]+E2.val[e];
		dp2(v);
	}
}
int findson(int v,int u){
	for(int k=19;k>=0;k--)
		if(deep[fa[v][k]]>deep[u]) v=fa[v][k];
	return v;
}
int search(int v,int dv,int u,int du){
	static int nearv,nearu,distov,distou;
	nearv=near[v]; nearu=near[u];
	for(int k=19;k>=0;k--) if(deep[fa[v][k]]>deep[u]){
		distov=dv+deep[v]-deep[fa[v][k]];
		distou=du+deep[fa[v][k]]-deep[u];
		if(distov<distou||(distov==distou&&nearv<nearu))
			dv=distov,v=fa[v][k];
	}
	return v;
}
void dp3(int u){
	int sum=0,x,y;
	for(int e=E2.head[u];e;e=E2.nxt[e]){
		int v=E2.to[e]; x=findson(v,u); sum+=size[x];
		if(near[v]==near[u]) ANS[near[u]]+=size[x]-size[v];
		else{
			y=search(v,dis[v],u,dis[u]);
			ANS[near[u]]+=size[x]-size[y];
			ANS[near[v]]+=size[y]-size[v];
		}
		dp3(v);
	}
	ANS[near[u]]+=size[u]-sum;
	//reset these arrays
	E2.head[u]=0; near[u]=0; dis[u]=INF;
}
void solve(){
	static int a[MAXN],b[MAXN],stk[MAXN],top,lca;
	read(M); top=0; E2.ent=2;
	for(int i=1;i<=M;i++) read(a[i]),mark[a[i]]=1,b[i]=a[i];
	sort(a+1,a+M+1,cmp); stk[++top]=1;
	for(int i=1;i<=M;i++){
		lca=LCA(stk[top],a[i]);
		if(lca!=stk[top]) while(1){
			if(dfn[stk[top-1]]<=dfn[lca]){
				E2.Adde(lca,stk[top],deep[stk[top]]-deep[lca]),top--;
				if(stk[top]!=lca) stk[++top]=lca;
				break;
			}
			E2.Adde(stk[top-1],stk[top],deep[stk[top]]-deep[stk[top-1]]),top--;
		}
		if(stk[top]!=a[i]) stk[++top]=a[i];
	}
	while(top>1) E2.Adde(stk[top-1],stk[top],deep[stk[top]]-deep[stk[top-1]]),top--;
	dp1(1); dp2(1); //Get the nearest key vertex of each vertex on the virtual tree.
	dp3(1); //Get the answers.
	for(int i=1;i<=M;i++){
		printf("%d%c",ANS[b[i]],i==M?'\n':' ');
		ANS[b[i]]=0; mark[b[i]]=0;
	}
}
int main(){
	read(N);
	memset(dis,0x3f,sizeof(dis));
	for(int i=1,a,b;i<N;i++){
		read(a); read(b);
		E1.Adde(a,b,1); E1.Adde(b,a,1);
	}
	dfs(1,1); read(Q);
	while(Q--) solve();
	return 0;
}