数据挖掘入门系列教程（十二）之使用keras构建CNN网络识别CIFAR10

简介

在上一篇博客：数据挖掘入门系列教程（十一点五）之CNN网络介绍中，介绍了CNN的工作原理和工作流程，在这一篇博客，将具体的使用代码来说明如何使用keras构建一个CNN网络来对CIFAR-10数据集进行训练。

如果对keras不是很熟悉的话，可以去看一看官方文档。或者看一看我前面的博客：数据挖掘入门系列教程（十一）之keras入门使用以及构建DNN网络识别MNIST，在数据挖掘入门系列教程（十一）这篇博客中使用了keras构建一个DNN网络，并对keras的做了一个入门使用介绍。

CIFAR-10数据集

CIFAR-10数据集是图像的集合，通常用于训练机器学习和计算机视觉算法。它是机器学习研究中使用比较广的数据集之一。CIFAR-10数据集包含10 种不同类别的共6w张32x32彩色图像。10个不同的类别分别代表飞机，汽车，鸟类，猫，鹿，狗，青蛙，马，轮船 和卡车。每个类别有6,000张图像

在keras恰好提供了这些数据集。加载数据集的代码如下所示：

from keras.datasets import cifar10

(x_train, y_train), (x_test, y_test) = cifar10.load_data()

print(x_train.shape, 'x_train samples')
print(x_test.shape, 'x_test samples')
print(y_train.shape, 'y_trian samples')
print(y_test.shape, 'Y_test samples')

输出结果如下：

训练集有5w张图片，测试集有1w张图片。在\(x\)数据集中，图片是\(（32，32，3)\)，代表图片的大小是\(32 \times 32\)，为3通道（R,G,B）的图片。

展示图片内容

我们可以稍微的展示一下图片的内容，python代码如下所示：

import matplotlib.pyplot as plt
%matplotlib inline

plt.figure(figsize=(12,10))
x, y = 8, 6

for i in range(x*y):
    plt.subplot(y, x, i+1)
    plt.imshow(x_train[i],interpolation='nearest')
plt.show()

下面就是数据集中的部分图片：

数据集变换

同样，我们需要将类标签进行one-hot编码：

import keras
# 将类向量转换为二进制类矩阵。
y_train = keras.utils.to_categorical(y_train, 10)
y_test = keras.utils.to_categorical(y_test, 10)

实际上这一步还有很多牛逼（骚）操作，比如说对数据集进行增强，变换等等，这样都可以在一定程度上提高模型的鲁棒性，防止过拟合。这里我们就怎么简单怎么来，就只对数据集标签进行one-hot编码就行了。

构建CNN网络

构建的网络模型代码如下所示：

from keras.models import Sequential
from keras.layers import Dense, Dropout, Activation, Flatten,Conv2D, MaxPooling2D

# 构建CNN网络
model = Sequential()

# 添加卷积层
model.add(Conv2D(32, (3, 3), padding='same',input_shape=x_train.shape[1:]))
# 添加激活层
model.add(Activation('relu'))
model.add(Conv2D(32, (3, 3)))
model.add(Activation('relu'))

# 添加最大池化层
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))

model.add(Conv2D(64, (3, 3), padding='same'))
model.add(Activation('relu'))
model.add(Conv2D(64, (3, 3)))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))

# 将上一层输出的数据变成一维
model.add(Flatten())
# 添加全连接层
model.add(Dense(512))
model.add(Activation('relu'))
model.add(Dropout(0.5))
model.add(Dense(10))
model.add(Activation('softmax'))

# 网络模型的介绍
print(model.summary())

这里解释一下代码：

Conv2D

Conv2D代表2D的卷积层，可能这里会有人问，我的图片不是3通道（RGB）的吗？为什么使用的是Conv2D而不是Conv3D。首先先说明，在Conv2D中的这个“2”代表的是卷积层可以在两个维度（也就是width,length）进行移动。那么同理Conv3D中的“3”代表这个卷积层可以在3个维度进行移动（比如说视频中的width ，length，time）。那么针对RGB这种3通道（channels），卷积过程中输入有多少个通道，则滤波器（卷积核）就有多少个通道。

简单点来说就是：

输入

单色图片的input，是2D， \(w \times h\)

彩色图片的input，是3D，\(w \times h \times channels\)

卷积核filter

单色图片的filter，是2D, \(w \times h\)

彩色图片的filter，是3D, \(w \times h \times channels\)

值得注意的是，卷积之后的结果是二维的。（因为会将3维卷积得到的结果进行相加）

接着继续解释Conv2D的参数：

Conv2D(32, (3, 3), padding='same',input_shape=x_train.shape[1:])

• 32表示的是输出空间的维度（也就是filter滤波器的输出数量）
• （3，3）代表的是卷积核的大小
• strides(这里没有用到)：这个代表是滑动的步长。
• input_shape：输入的维度，这里是（28,28,3）

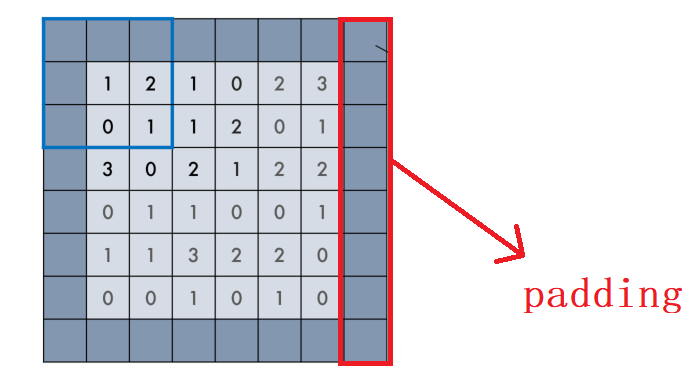
padding在上一篇博客介绍过，在keras中有两个取值："valid" 或 "same" (大小写敏感)。

• valid padding：不进行任何处理，只使用原始图像，不允许卷积核超出原始图像边界
• same padding：进行填充，允许卷积核超出原始图像边界，并使得卷积后结果的大小与原来的一致

Flatten

Flatten这一层就是为了将多维数据变成一维数据：

构建网络

from keras.optimizers import RMSprop
# 利用 RMSprop 来训练模型。
model.compile(loss='categorical_crossentropy',
              optimizer=RMSprop(),
              metrics=['accuracy']
             )

其他的参数在上两篇博客中已经讲了，就不再赘述。

进行训练评估

这里大家可以根据自己的电脑配置适当调整一下batch_size的大小。

history = model.fit(x_train, y_train,
                    batch_size=32,
                    epochs=64,
                    verbose=1,
                    validation_data=(x_test, y_test)
                   )

在i5-10代u，mx250的情况下，训练一轮大概需要27s左右。

训练完成之后，进行评估：

score = model.evaluate(x_test, y_test, verbose=0)
print('Test loss:', score[0])
print('Test accuracy:', score[1])

结果如下所示：

这个结果可以说的上是一言难尽，