zabbix3.4.x添加短信报警
一、修改zabbix_server.conf
#vi /etc/zabbix/zabbix_server.conf
去掉注释: ### Option: AlertScriptsPath
# Full path to location of custom alert scripts.
# Default depends on compilation options.
#
# Mandatory: no
# Default:
# AlertScriptsPath=${datadir}/zabbix/alertscripts AlertScriptsPath=/usr/lib/zabbix/alertscripts
二、编写脚本上传到上面的目录
#!/usr/bin/env python
# *-* coding:utf-8 *-*
import hashlib,urllib,urllib2,sys,time,requests class REST_API:
def __init__(self):
self.ip = '118.190.103.79'
self.user='ld1978'
self.password = ''
# self.md5_pwd = hashlib.md5(self.password.encode('utf-8')).hexdigest()
# self.author = base64.b64encode(self.user + ':' + self.md5_pwd) def msm_sign(self): return hashlib.md5( "%s%s%s"%(self.user,self.password,time.strftime("%Y%m%d%H%M%S", time.localtime()))).hexdigest()
def req_url(self,phone, content):
content = '%s 【glp-zabbix】'%content data = {
'userid': 3442,
'timestamp':time.strftime("%Y%m%d%H%M%S", time.localtime()),
'content': content, # yes;内容
'mobile': phone, # yes;现只支持sms
'sendTime': '', # no;定时发送时间
'extno': '',
'sign':self.msm_sign() #sign
} #data_re = urllib.urlencode(data)
url = 'http://%s/v2sms.aspx?action=send' % (self.ip)
response = requests.get(url, params=data) data = response.text if(data.find('Success') >=0):
print "Success"
else:
print "Faild" if __name__ == '__main__': sms = REST_API()
send_to = str(sys.argv[1])
message = str(sys.argv[2])
print type(send_to)
sms.msm_sign()
# 多个号码用,隔开像 189
sms.req_url(send_to,message)
sendsms.py
三、在Administration->Media types下新增Media,并增加两个参数
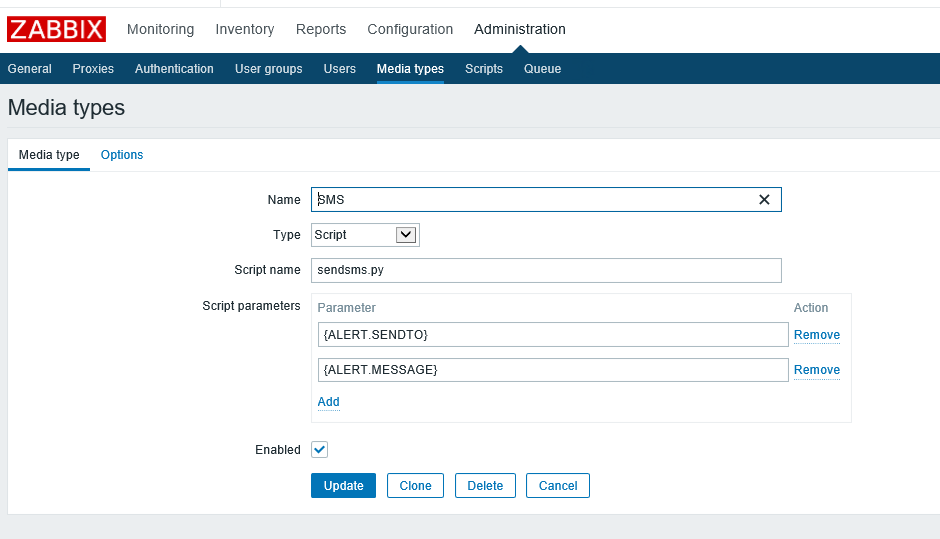
四、增加Action
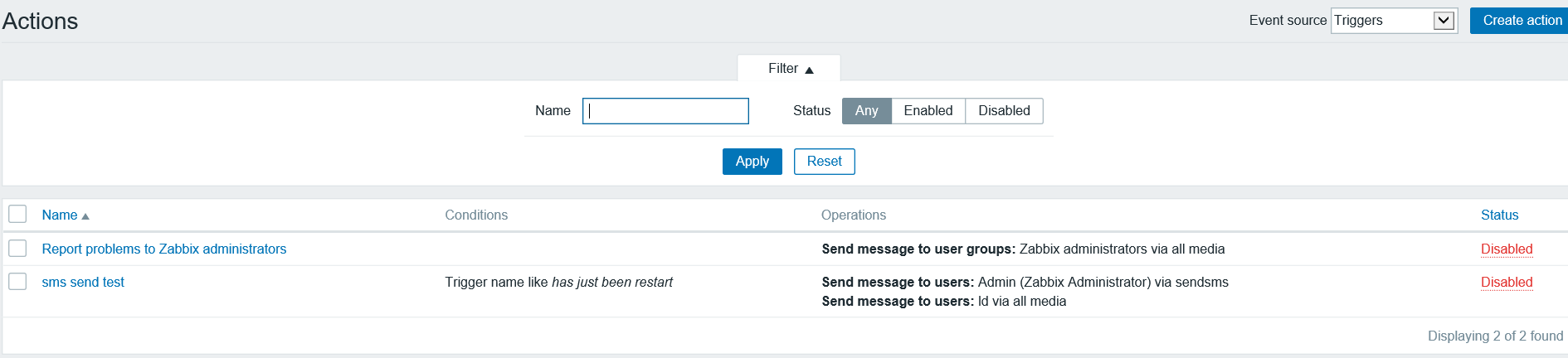
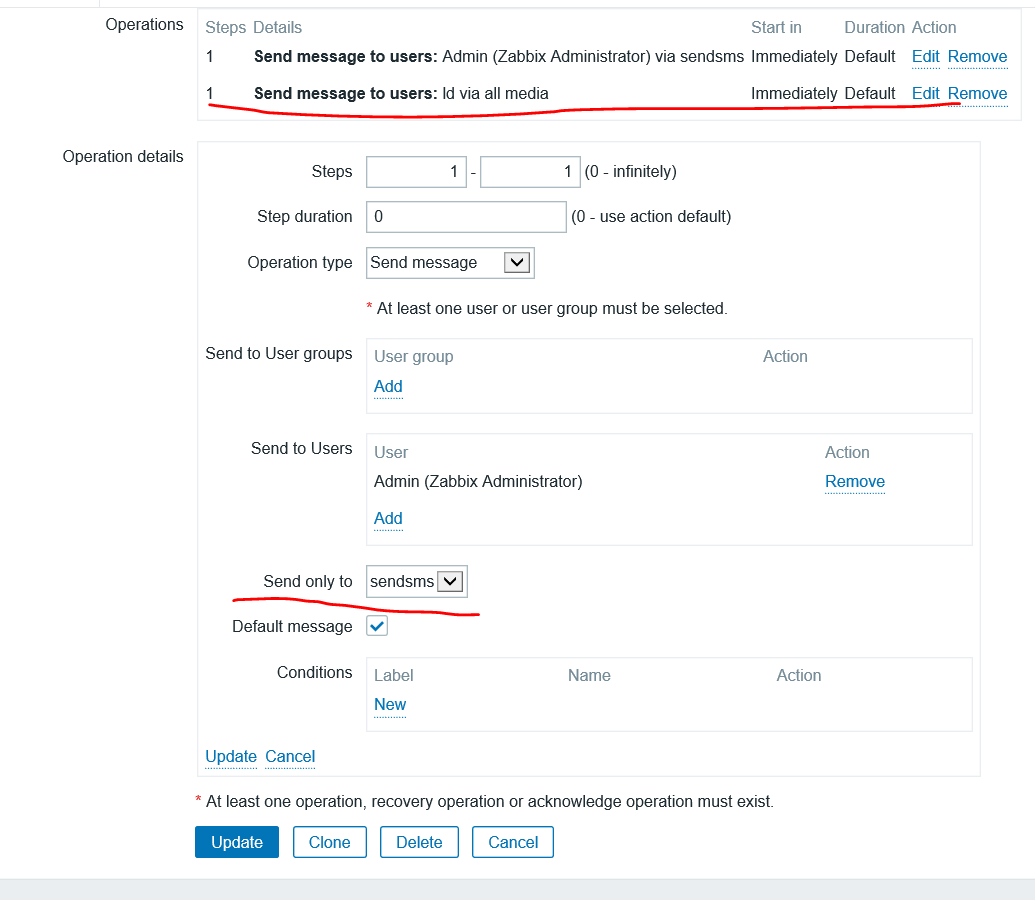
zabbix3.4.x添加短信报警的更多相关文章
- Grafana 短信报警
一.分析 需求 Grafana支持短信渠道报警 要求 使用开发提供的短信API接口 请求url: http://192.168.1.1:8088/alerting/sendSms?mobile=手机号 ...
- zabbix学习笔记:zabbix监控之短信报警
zabbix学习笔记:zabbix监控之短信报警 zabbix的报警方式有多种,除了常见的邮件报警外,特殊情况下还需要设置短信报警和微信报警等额外方式.本篇文章向大家介绍短信报警. 短信报警设置 短信 ...
- zabbix3配置短信报警
需求:在zabbix服务器配置短信报警,当服务出现故障达到预警级别是通过发送短信的形式告诉运维人员,以便及时处理. 一.zabbix服务器端配置短信脚本 我的短信脚本放置位置为 /etc/zabbix ...
- CactiEZ 中文版V10.1安装使用以及139邮箱短信报警设置
说明:CactiEZ中文版V10.1是基于CentOS 6.0系统,整合Cacti等相关软件,重新编译而成的一个操作系统! 说明:CactiEZ中文版V10.1是基于CentOS 6.0系统,整合 ...
- centos7之zabbix邮件报警(短信报警)
前言 前面我们介绍了zabbix的基本linux和window及SNMP流量的简单监控,我们知道作为运维人员,需要7x24小时待命,但是我们不可能时时刻刻都坐在电脑旁边查看监控上的各个主机状态,所以我 ...
- zabbix系列之十——添加短信告警
zabbix添加短信告警 1.查看zabbix-server脚本存放路径: [root@GYQ-Prod-Zabbix ~]# grep AlertScriptsPath /etc/zabbix/za ...
- zabbix 短信报警
使用的短信平台是云片网,接口请看官网短信接口API文档,有示例 进入server服务器存放脚本的文件夹,默认路径是 [root@test zabbix]# cat zabbix_server.conf ...
- Zabbix 短信报警示例
Zabbix 短信报警 示例: 注意zabbix 脚本文件默认放置目录是 alertscripts (zabbix 动作调用脚本目录) # 编辑 zabbix_server.conf # AlertS ...
- server宕机监控、检測、报警程序(139绑定手机短信报警)monitor_down.sh
宕机监控报警程序 一. 需求来源 宕机对运维人员来说,最痛苦了.怎样检測一台server是否还在正常执行,假设该server宕机,怎样在第一时间监測到并通知一线运维人员进行维护,最大化降低损失. ...
随机推荐
- 状态模式(State)(开关灯,状态实例为类,不同状态,不同行为)
(当一个对象内在状态改变时允许其改变行为,这个对象看起来像改变了其类.) 在软件开发过程中,很多对象也会像水和信号灯一样具有多种状态,这些状态在某些情况下能够相互转换,而且对象在不同的状态下也将有不同 ...
- qml获取实际渲染的字体
当设置qml的Text元素的字体时,如果系统中不存在设置的字体,qml会根据匹配算法自动选取系统中存在的一种字体.比如:设置font.family: "微软雅黑",但系统中根本没有 ...
- springboot实现定时任务的方式
springboot实现定时任务的方式 a Timer:这是java自带的java.util.Timer类,这个类允许你调度一个java.util.TimerTask任务.使用这种方式可以让你的程 ...
- npm install时出现error
今天启动vue前端时,发现依赖没了.于是乎cmd->npm install->更新了部分依赖后,出现error信息,提示更新依赖失败.很奇怪,原来这个项目都是好的,为啥突然更新下来依赖了呢 ...
- javascript基础:语法与html结合方式
一.基本语法: 1.与html结合方式 1.内部JS: * 定义<script>,标签体内容就是JS代码 2.外部JS: * 定义<script>,通过src属性引入外部的 ...
- loj6402 校门外的树(dp,多项式求逆)
https://loj.ac/problem/6402 庆祝一下,,,第一个我自己做出来的,,,多项式的题(没办法,我太弱 虽然用了2个小时才想出来,但这毕竟是0的突破…… 首先声明,虽然我写的题解很 ...
- Chai.js断言库API中文文档
基于chai.js官方API文档翻译.仅列出BDD风格的expect/should API.TDD风格的Assert API由于不打算使用,暂时不放,后续可能会更新. BDD expect和shoul ...
- light7结合jquery实现开关按钮
<!DOCTYPE html> <html> <head> <meta charset="utf-8"> <meta http ...
- Hdu 1384(差分约束)
题目链接 Intervals Time Limit: 10000/5000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)T ...
- 前言-使用Eclipse创建SpringBoot项目
1.首先我们需要安装STS插件:Help--> Eclipse Marketplace 2. 然后 File-->New--->Spring Starter Project 3.下 ...
