【笔记】机器学习 - 李宏毅 - 4 - Gradient Descent

梯度下降 Gradient Descent
梯度下降是一种迭代法（与最小二乘法不同），目标是解决最优化问题：\({\theta}^* = arg min_{\theta} L({\theta})\)，其中\({\theta}\)是一个向量，梯度是偏微分。

为了让梯度下降达到更好的效果，有以下这些Tips：

1.调整学习率

梯度下降的过程，应当在刚开始的时候，应该步长大一些，以便更快迭代，当靠近目标时，步长调小一些。
虽然式子中的微分有这个效果，但同时改变一下学习率的值，可以很大程度加速这个过程。
比如说用 \(1/t\) 衰减：\({\eta}^t = {\eta}/\sqrt{(t + 1)}\)
另外，不同的参数应当给不同的学习率。

Adagrad方法
Adagrad是再除以一个参数之前所有微分的均方根。

消去\(\sqrt{(t + 1)}\)参数后得到：

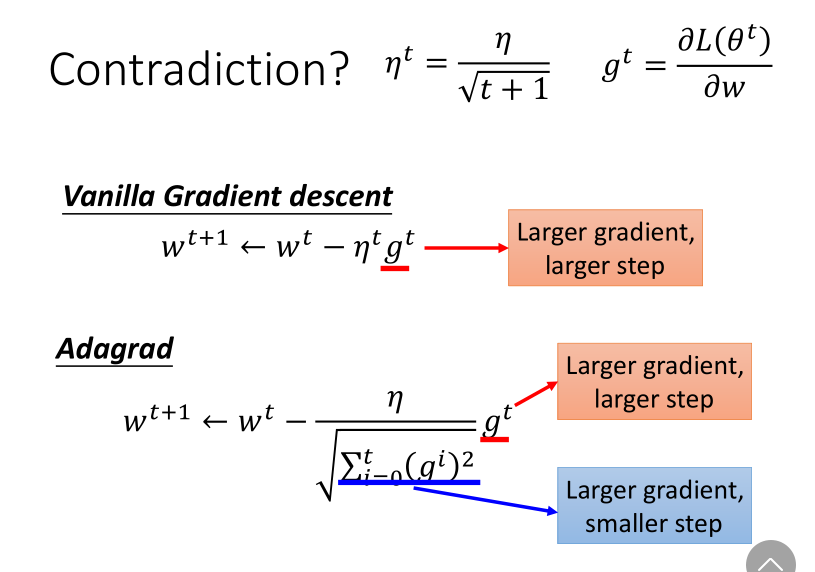
分子分母的作用形成了反差，一个增加步长，一个减小步长。

对此的一种解释是，为了避免迭代突然加快，或者突然减慢。

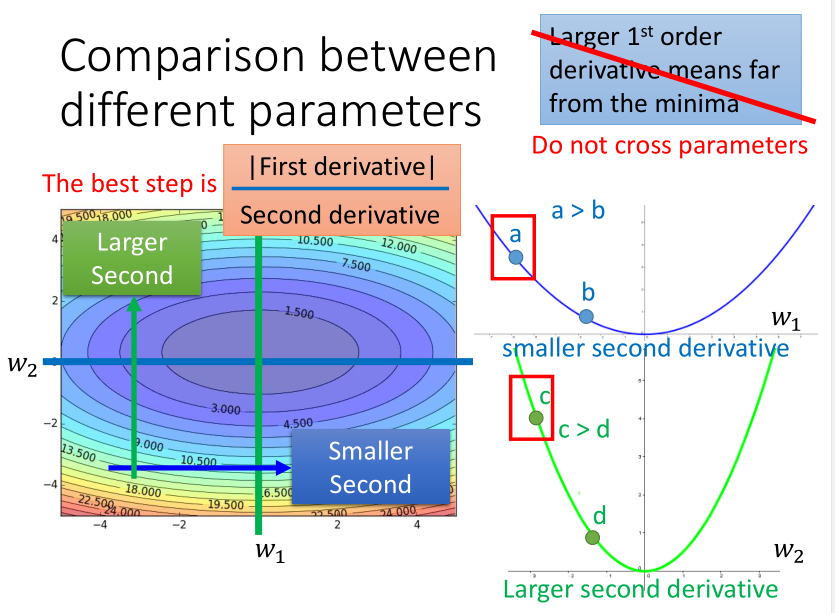
另外一种解释是，以二次凸函数举例，最佳迭代步长直观看是与一次微分成正比的。
但如果考虑跨参数比较的话（不仅看\(x\)），又会发现这个结论不完善，其实它又与二次微分成反比，所以要综合考虑两者。
而二次微分比较难计算，需要更多的时间，所以一般就采用一次微分的均方根来模拟它了。

2.随机梯度下降

随机梯度下降和批量梯度下降不同的是，它不需要把所有训练数据都考虑进来再迭代，而是算出其中一个样本的梯度就迭代一次。
这种方法虽然很快，但数据的震荡也很明显。（小批量梯度下降mini-batch gradient descent是算出其中一部分样本的梯度，是一种折中方法）

3.特征缩放

两个参数的变化范围不同，则在考虑学习率的时候需要分别考虑，比较难处理，而右边的情形就比较容易更新参数，这就是进行特征缩放的原因。
最常见的做法就是直接将其正则化。

梯度下降的原理
为什么每次迭代时，损失函数一定会变小呢？不一定。

可以用泰勒公式可以做解释，一阶的形式非常类似，无论是微分还是偏微分。所以只有当步长较小时，才符合条件。

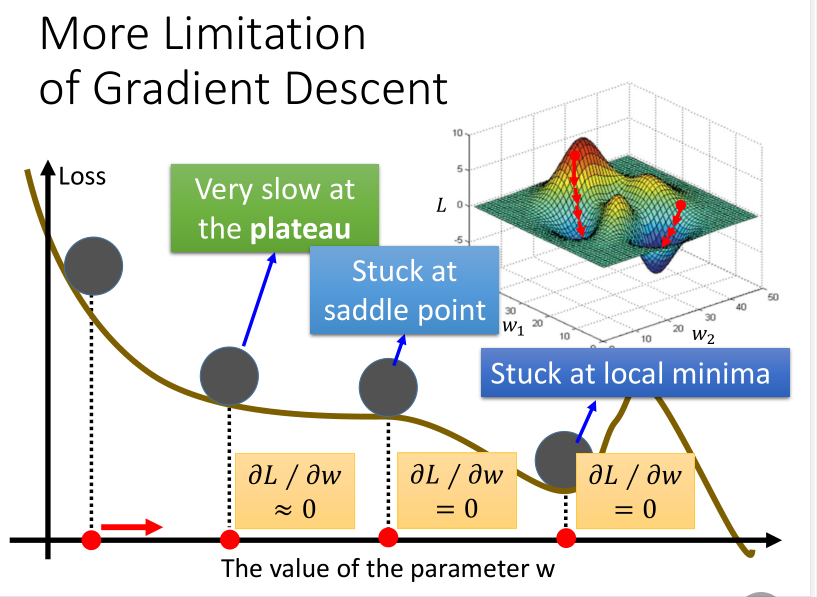
梯度下降的局限

梯度下降方法也有它自身的局限性，如下图所示：