CCPC 2019 网络赛 HDU huntian oy （杜教筛）

1005 huntian oy （HDU 6706）

题意：

令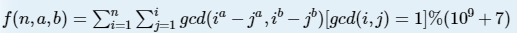，有T次询问，求 f(n, a, b)。

其中 T = 10^4，1 <= n，a，b <= 1e9，保证每次 a，b互质。

思路：

首先我们需要知道

公式：　　gcd(a^n - b^n, a^m - b^m) = a^(gcd(m,n)) - b^(gcd(m,n))

由a，b互质，原式即为

　　　　　　f(n, a, b) = ∑∑ (i-j)*[(i,j)=1] = ∑ (i*∑ [(i, j)=1] ) - ∑∑ j*[(i, j)=1]

然后我们还要知道

欧拉函数定义式：　　　　phi(n) =  ∑ [(i, n)=1]

1…n中与n互质的数的和： ∑ i*[(i, n)=1] = phi(n)*n / 2，n>1，(n==1时 和为1)

所以

　　　　　　f(n, a, b) = ∑ i*phi(i) - (∑ phi(i)*i/2 + 1/2) = (∑ i*phi(i)  - 1) / 2

现在问题变成 求 i*phi(i) 的前缀和。由于 n 很大，达到 10^9，线性时间是不够的，要用到杜教筛。

不懂杜教筛？出门右拐先去这篇博客研究研究。学会了可以先尝试本篇博客后面的模板题：洛谷P4213。

预处理 √n 以内的前缀和后，剩下部分利用整除分块求解的时间复杂度为 O(n^(3/4))，预处理前 k = n^(2/3) 时 时间复杂度可以优化到 O(n^(2/3))。详见大佬的博客分析。

AC代码：

#include <cstdio>
#include <unordered_map>
using namespace std;
const int mod = 1e9+;
const int MAXN = ;

unordered_map<int, long long> Sumiphi;
int prime[MAXN+], cnt;
long long phi[MAXN+];
long long iphi[MAXN+];
bool isprime[MAXN+];

// 线性筛
void getPrime(int n) {
    isprime[] = true;
    phi[] = ;
    for(int i=;i<=n;i++) {
        if(!isprime[i])
            prime[++cnt] = i, phi[i] = i-;

        for(int j=;j<=cnt&&prime[j]*i<=n;j++) {
            isprime[prime[j]*i] = true;
            phi[prime[j]*i] = phi[i]*(prime[j]-);
            if(i%prime[j]==) {
                phi[prime[j]*i] = phi[i]*(prime[j]);
                break;
            }
        }
    }
    // 前缀和
    for(int i=;i<=n;i++) {
        iphi[i] = iphi[i-] + phi[i]*i % mod;
        iphi[i] %= mod;
    }
}

const int _two = (+mod)/;
const int _six = ;

// 杜教筛求 ∑i*phi(i)
// S(n) = ∑i^2 - ∑d*S(n/d) = n*(n+1)*(2n+1)/6 - ∑d×S(n/d)
long long iphiSum(int n) {
    if(n<=MAXN)
        return iphi[n];
    if(Sumiphi.count(n))
        return Sumiphi[n];

    long long sum = ;
    for(int i=,j;i<=n;i=j+) {
        j = n/(n/i);
        sum += iphiSum(n/i)*(j-i+)% mod *(i+j) % mod *_two % mod;
    }
    Sumiphi[n] = ((1LL*n*(n+)% mod *(*n+)% mod *_six % mod - sum)%mod + mod) % mod;
    return Sumiphi[n];
}

// 答案：
// ( Sum(i*phi(i)) - 1 ) /2
int main() {
    getPrime(MAXN);
    int T, n, a, b;
    scanf("%d", &T);
    while(T--) {
        scanf("%d %d %d", &n, &a, &b);
        printf("%lld\n", (iphiSum(n)-+mod)%mod * _two % mod);
    }
    return ;
}

P4213 【模板】杜教筛（Sum）

题意：

给定一个正整数 N (N<=2^31-1)，求

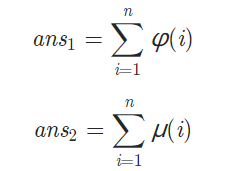
AC模板：

#include <cstdio>
#include <unordered_map>
using namespace std;
// 参考自：https://www.cnblogs.com/dreagonm/p/10077979.html

const int MAXN = ;
unordered_map<int, long long> Sumphi;
unordered_map<int, long long> Summu;
int prime[MAXN+], cnt;
long long mu[MAXN+], phi[MAXN+];
bool isprime[MAXN+];

// 线性筛
void getPrime(int n) {
    isprime[] = true;
    mu[] = ;
    phi[] = ;
    for(int i=;i<=n;i++) {
        if(!isprime[i])
            prime[++cnt] = i, phi[i] = i-, mu[i] = -;

        for(int j=;j<=cnt&&prime[j]*i<=n;j++) {
            isprime[prime[j]*i] = true;
            mu[prime[j]*i] = -mu[i];
            phi[prime[j]*i] = phi[i]*(prime[j]-);
            if(i%prime[j]==) {
                mu[prime[j]*i] = ;
                phi[prime[j]*i] = phi[i]*(prime[j]);
                break;
            }
        }
    }
    // 前缀和
    for(int i=;i<=n;i++) {
        mu[i] += mu[i-];
        phi[i] += phi[i-];
    }
}

// 杜教筛求 ∑u(i)
// S(n) = 1 - ∑S(n/d)
long long muSum(int n) {
    if(n<=MAXN)
        return mu[n];
    if(Summu.count(n))
        return Summu[n];

    int sum = ;
    for(int i=,j;i<=n;i=j+) {
        j = n/(n/i);
        sum += (j-i+)*muSum(n/i);
    }
    Summu[n] =  - sum;
    return Summu[n];
}

// 杜教筛求 ∑phi(i)
// S(n) = ∑ i - ∑S(n/d)
long long phiSum(int n) {
    if(n<=MAXN)
        return phi[n];
    if(Sumphi.count(n))
        return Sumphi[n];

    long long sum = ;
    for(int i=,j;i<=n;i=j+) {
        j = n/(n/i);
        sum += (j-i+)*phiSum(n/i);
    }
    Sumphi[n] = 1LL*(n+)*n/ - sum;
    return Sumphi[n];
}

int main() {
    getPrime(MAXN);
    int T, n;
    scanf("%d", &T);
    while(T--) {
        scanf("%d", &n);
        printf("%lld %d\n", phiSum(n), muSum(n));
    }
    return ;
}