HDU 1542 Atlantis（扫描线算法）

题意：给出n个矩形的左下角左边和右上角坐标，求这n个矩形的面积并

原题链接：http://acm.hdu.edu.cn/showproblem.php?pid=1542

---

典型的扫描线算法的题目

什么是扫描线？

顾名思义，扫描线就是用一根平行于x轴或y轴的线，把所有矩形都扫过去，并在这个过程逐渐把这些矩形的面积并求出来，下图给了平行于y轴的线的扫描情形

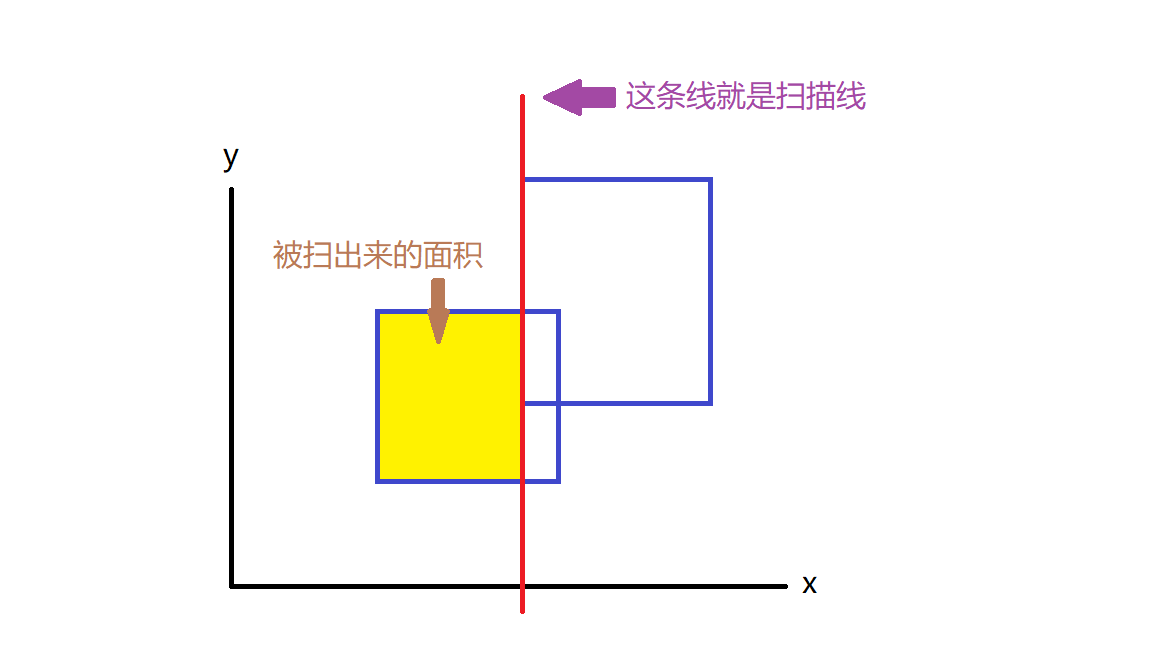
那么这条扫描线是怎么实现的呢？

以下讲述扫描线平行于y轴的情形

---

先说说扫描线的移动问题

第一步，坐标离散化

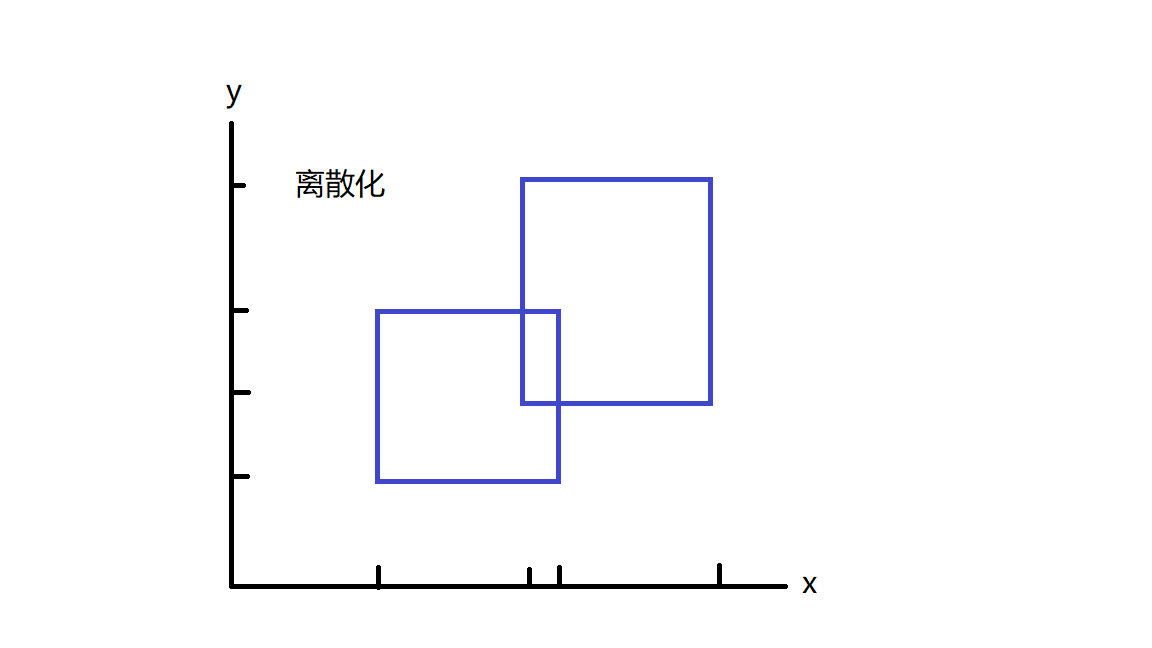
第二步，开始扫描

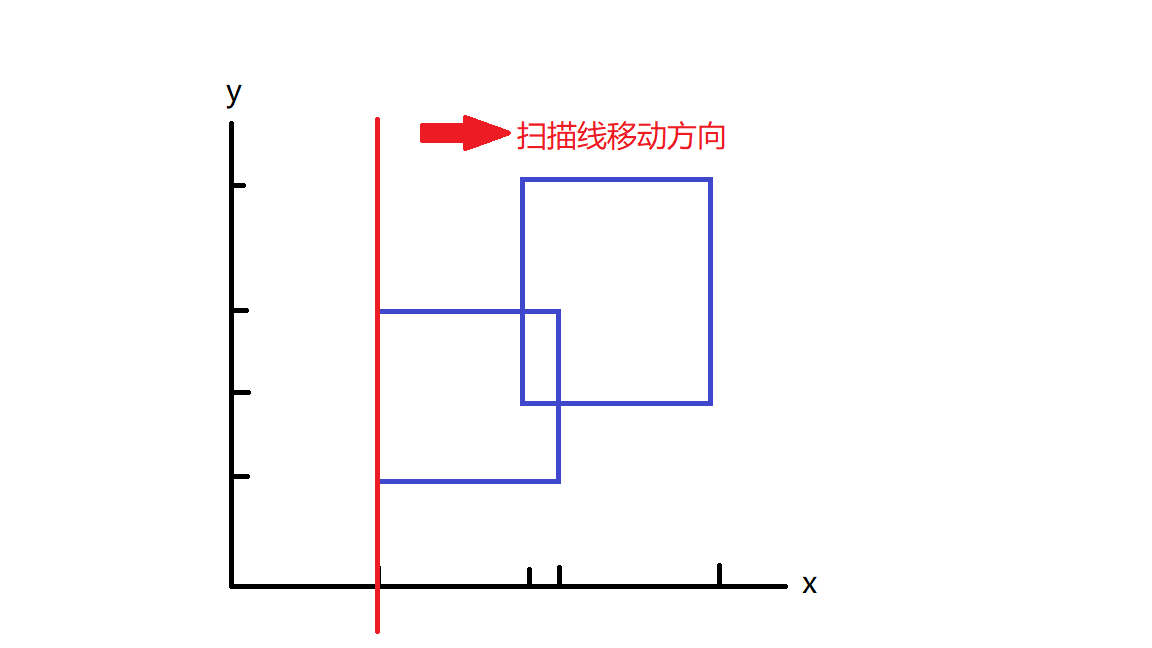
这根线顺着离散化后的x坐标挪就行了，这就是扫描线的移动方法

移动问题说完了，我们接下来说说怎么用这条线怎么把面积扫出来

目前这条线只是单纯的移动，并没什么用，也就是说这移动的过程中得附带一些操作，使得这条线有扫面积的功能才行，而这正是扫描线算法的难点。

在说明面积求法之前，先介绍两个概念，矩形的入边与矩形的出边

对于同一个矩形来说，先被扫描线扫到的边为入边，后被扫描线扫到的边为出边

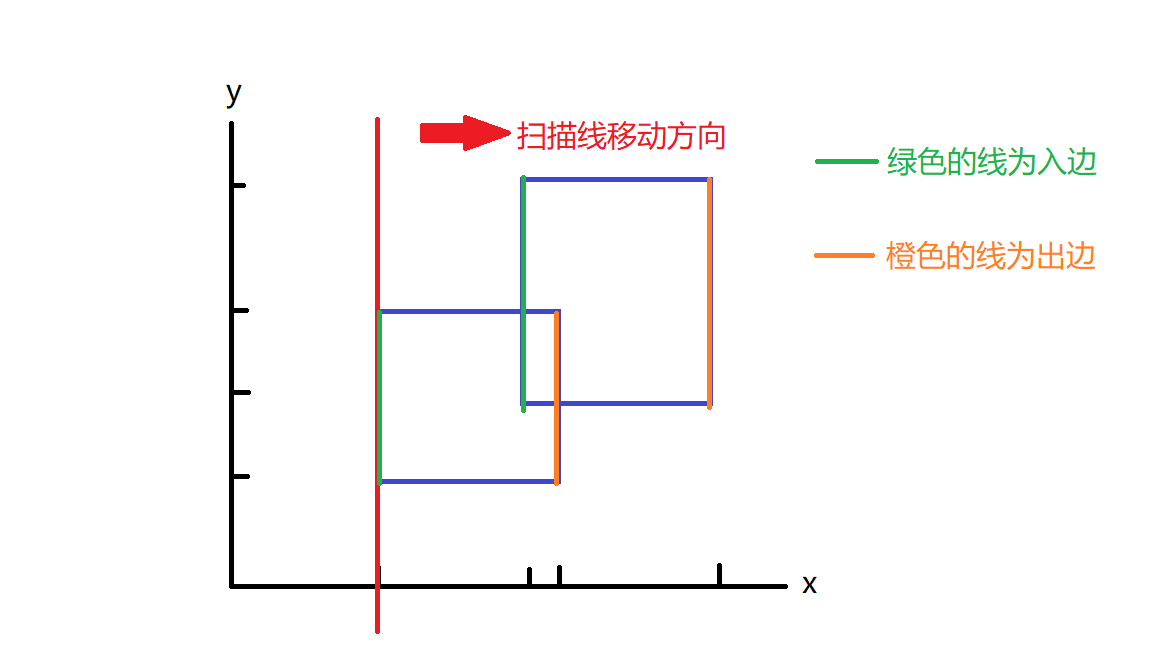
矩形上下的线呢？emmm......既然扫描线是平行y轴去移动的，那么矩形平行于x轴的边就没有用了，所以我们不管它，只看平行于y轴的边即可

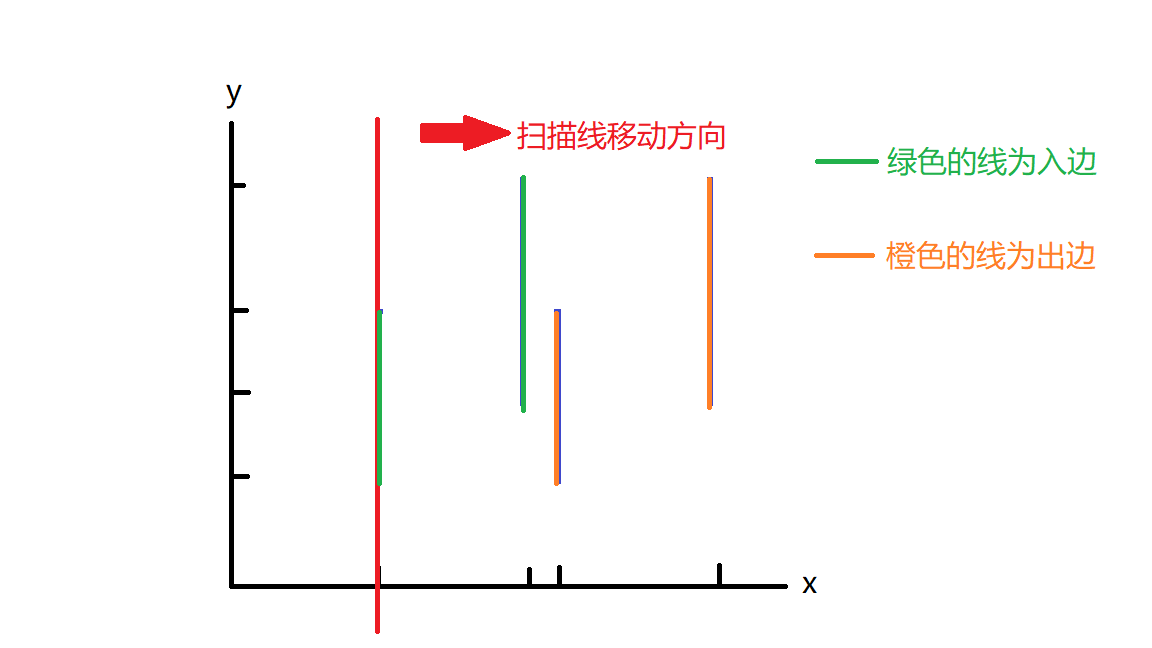
为了接下来扫描面积的说明方便，标下坐标轴的值

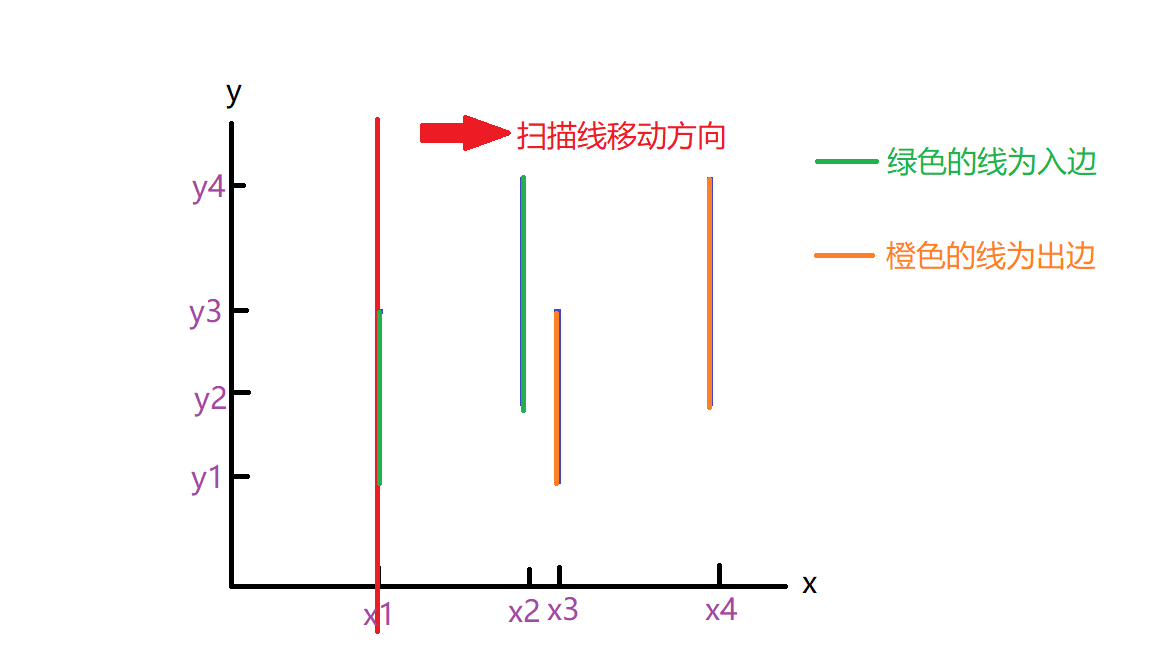
知道了入边出边的概念，这对求面积有什么用呢？

这涉及到有效覆盖线段的概念，扫描线扫到入边时，代表着那条入边的区间被覆盖，扫描到出边时，代表出边的区间被取消覆盖，注意，这里所说的覆盖是可以叠加的，比如扫到x2时，[y2, y3]就被覆盖了两次

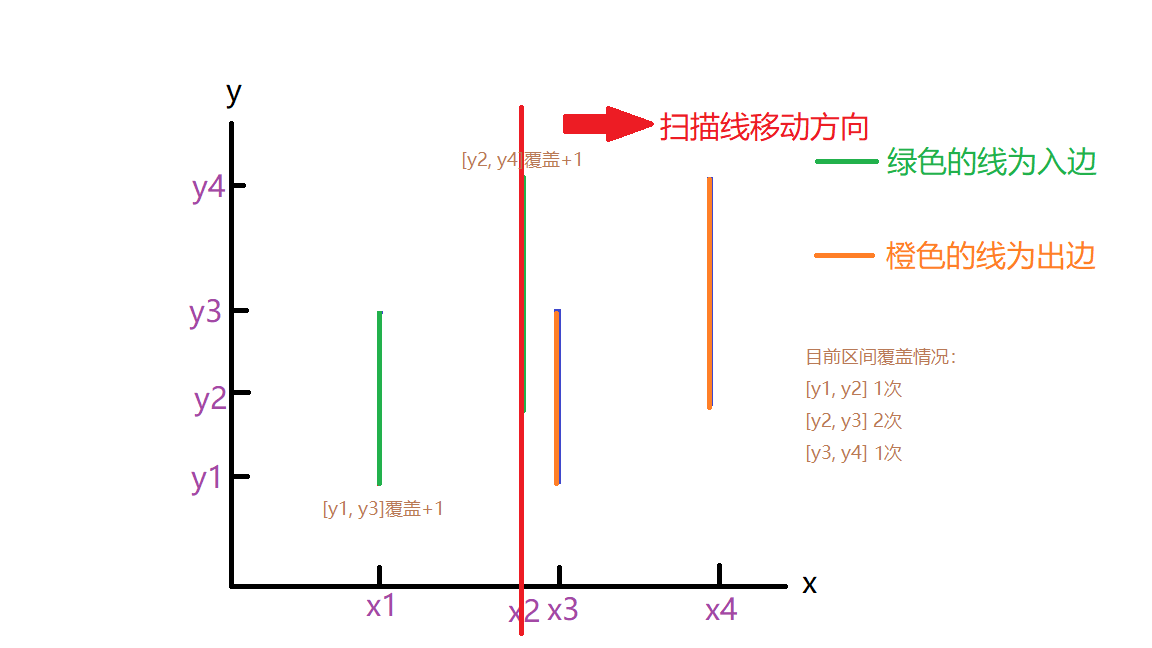
那么扫到x3，x4时情况也就分别如下图所示了

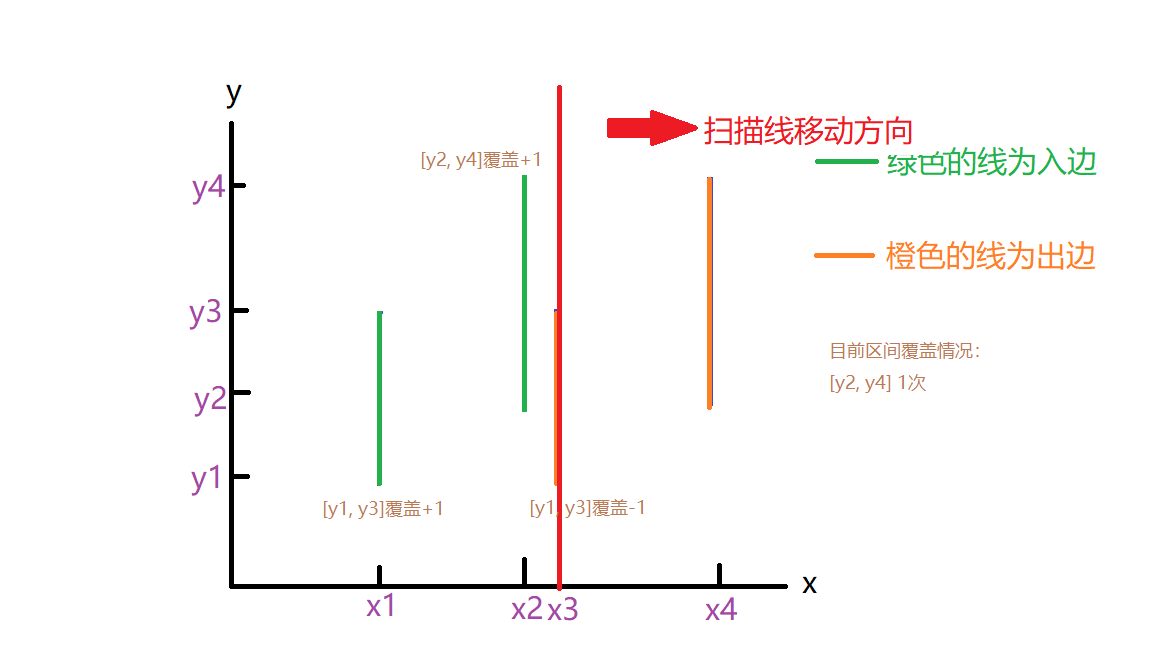
只要覆盖次数大于等于1的区间就是属于有效覆盖区间

那么面积跟这些覆盖区间有什么关系呢？其实是这样的，有效覆盖区间的长度应该就是扫描线所扫面积的宽度，也就是说，把扫描线看成刷子，当前有效的覆盖区间就是刷子下笔的地方，扫描线移动到下个x坐标上时，那整块区域就被刷上了，下面两张图给出从x1刷到x2的情形

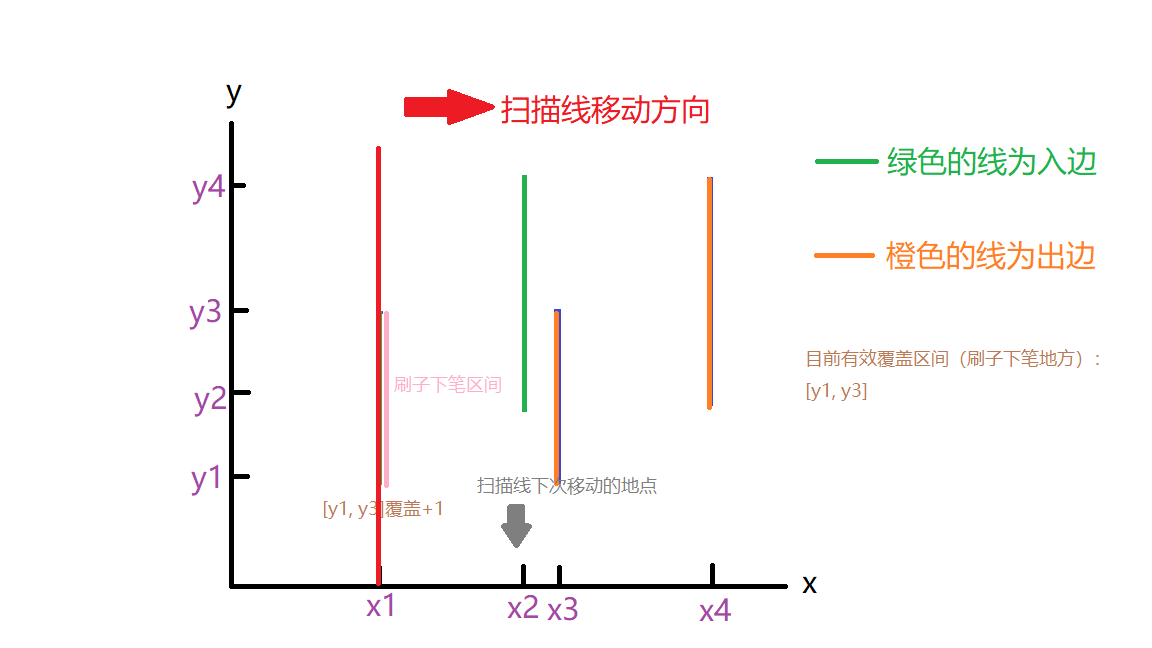
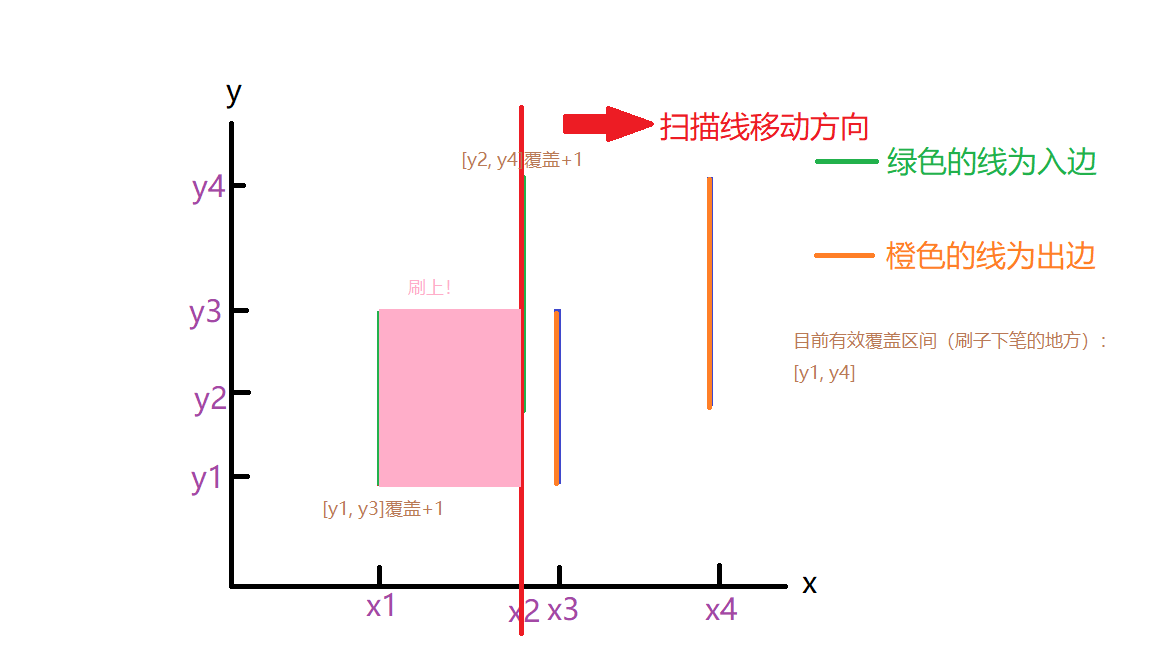
看，扫描线从x1挪到x2时，把x1到x2之间该求的面积刷上了，同时由于目前区间有效覆盖区间是[y1, y4]，这块地方又成为了下笔的区间，下面直接展示刷完所有矩形的过程

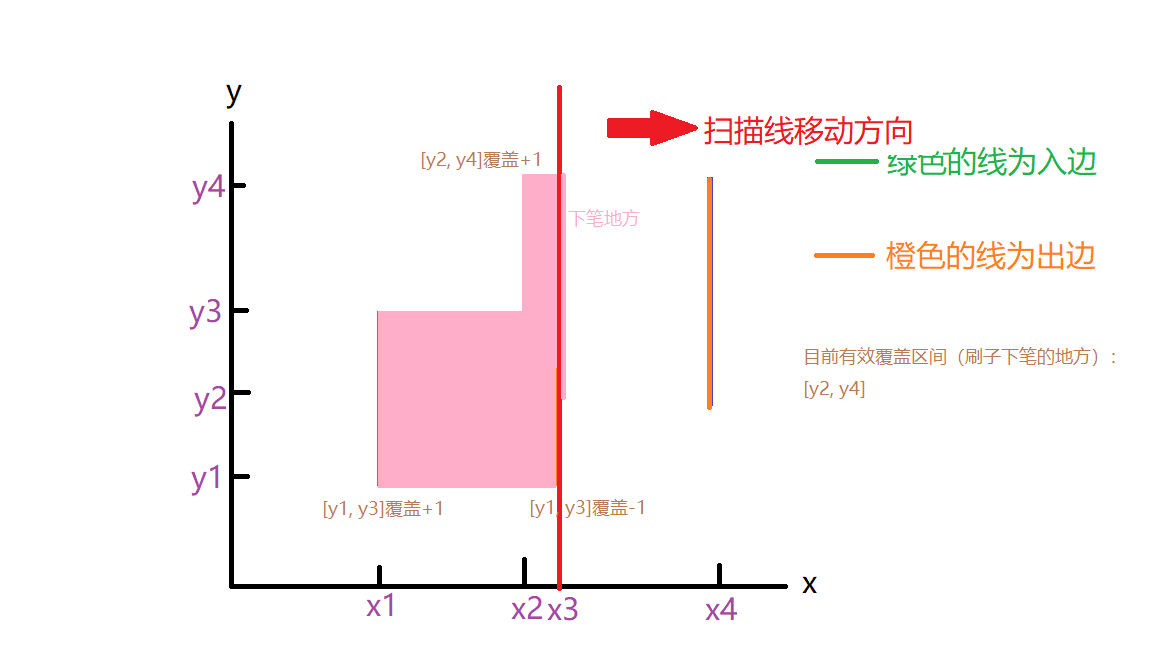
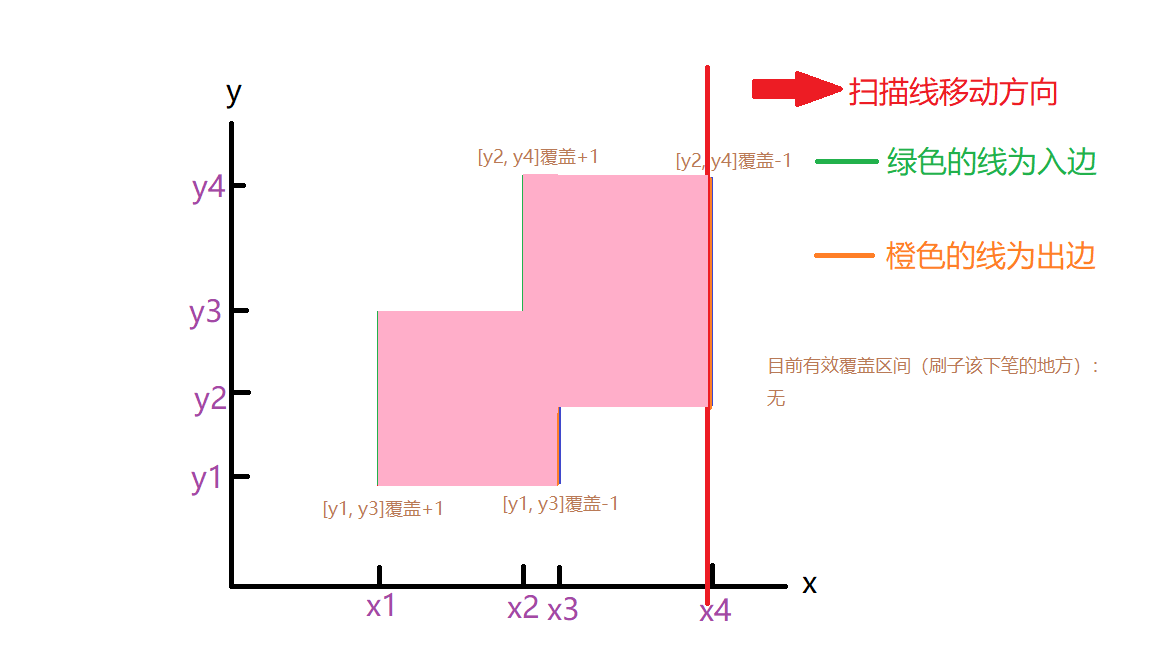
这样刷着刷着，刷完x4的时候全部矩形的并面积也就出来了

就这样，通过与有效覆盖区间的结合，扫描线就具备了求矩形并面积的功能

---

讲完这些，代码怎么实现呢？

涉及到区间覆盖，我们就用线段树去实现

坐标离散化后，把区间存入线段树中，根结点就是存了区间[y1, yn]

对于上面的例子，我们给出线段树的结构

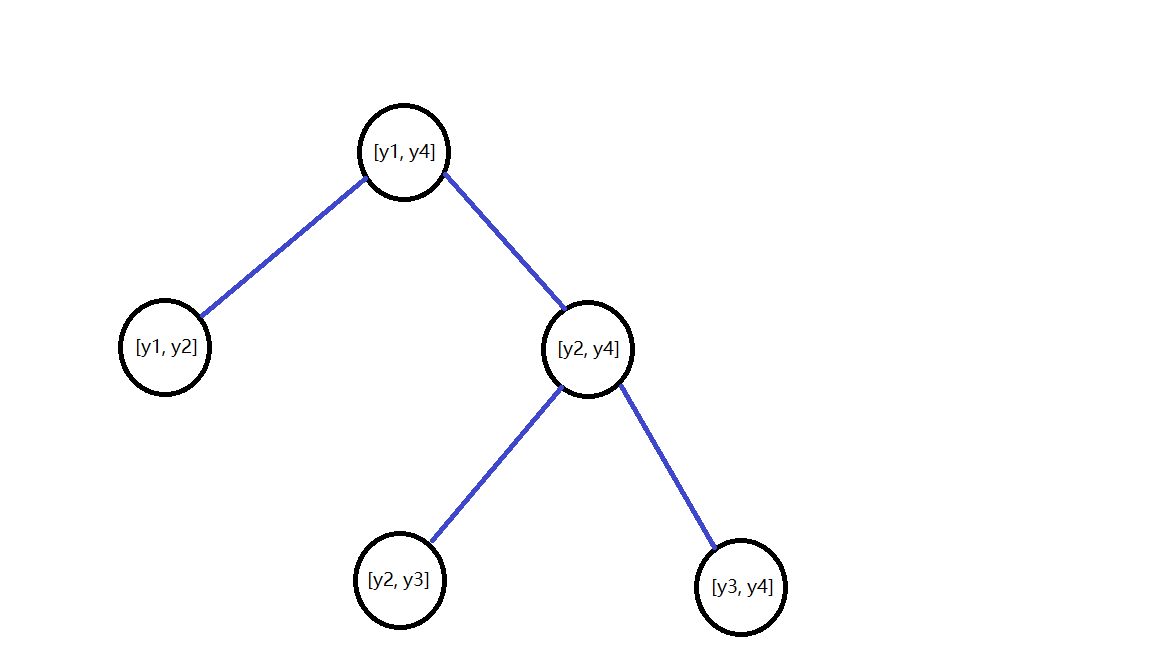
那么除了区间，我们还需要向结点中添加什么信息呢？

既然涉及到区间是否被覆盖，那么我们就得添加个区间是否被覆盖的标记（这里我给的标记名是res），由于覆盖可以叠加，那么我们这个标记就不能是简单的bool值，而是int值，表示被覆盖了多少次，同时若是扫描线扫到了入边，这个标记就+1，扫到出边就-1

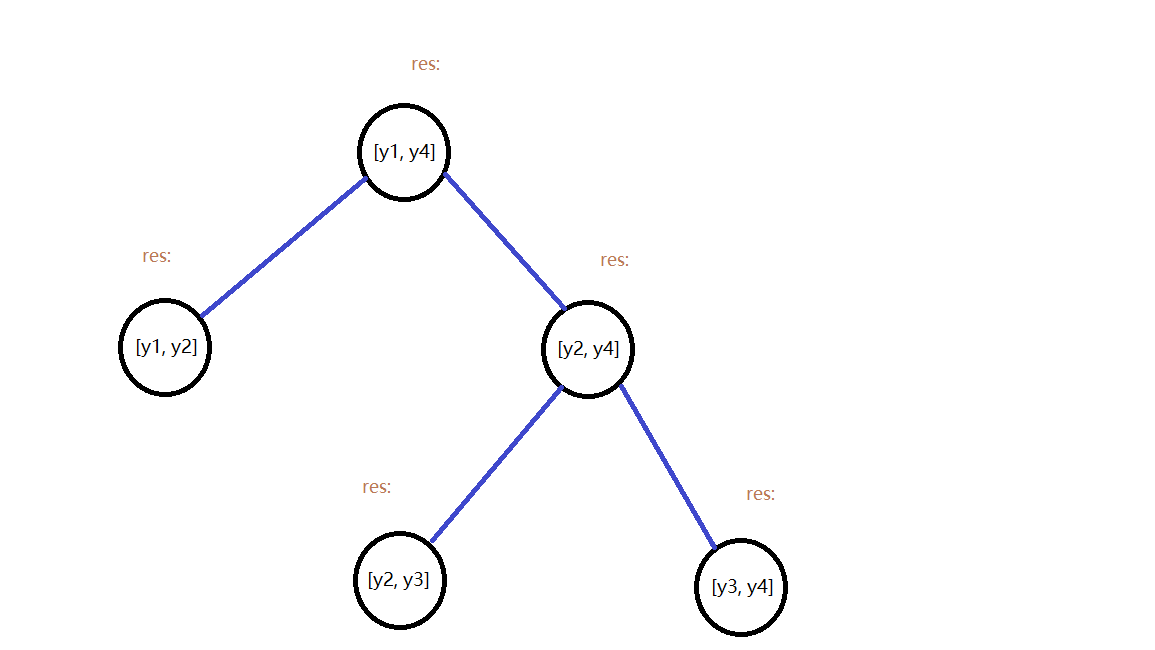
单单区间覆盖还不行，我们还得搞个有效覆盖区间的信息（这里我给的标记名是len），这个信息可以往上push_up，所以查询整个区间的有效覆盖长度时我们只需查询根结点就好，利用线段树的特性使得算法高效

所以，我们扫描线算法的核心就是扫描线在扫描过程中怎么维护线段树的res值跟len值

len值好维护，结点的res值大于等于1的话该节点的len就等于所管区间的长度，否则就是等于两个孩子的len值相加

那么res的值怎么维护呢？叶子结点好处理，只有区间被完全覆盖和完全不被覆盖两种情况，所以res就单纯的加加减减就好，但是树节点存在非完全覆盖的情况的，这就令树节点的res值很难处理了，如果是多个子节点合并着使得树节点所管区间被完全覆盖，那么这合并过程中每次都往子节点询问一次。最坏的情况下每次都得询问到叶子结点，这样线段树的高效性就没法体现出来。

有个解决的办法，那就是res值不要定义成该结点的区间被覆盖几次，而是定义成该结点的区间被直接完全覆盖了几次，什么意思呢？对于上面的线段树，你要是先覆盖[y2, y3]，再覆盖[y3, y4]，这时候[y2, y3]跟[y3, y4]这两个结点都是被直接覆盖的，它们的res值自然都是1，这时候[y2, y4]虽然时通过[y2, y3]跟[y3, y4]合并着被完全覆盖了，但是这并不属于直接覆盖，所以该结点的res = 0

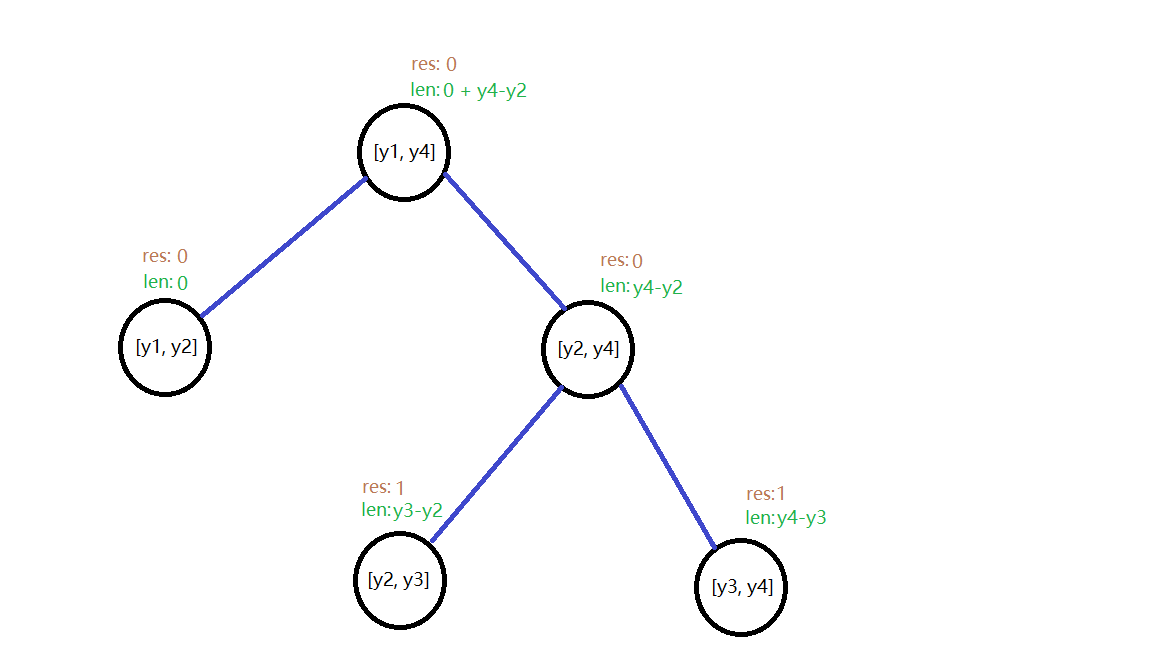
可是对于一来就覆盖[y1, y3]的情况呢？并没有直接管[y1, y3]的结点啊？我们分析知道在这个线段树结构中不管怎么处理，[y1, y3]必然都要被拆分成[y1, y2]和[y3, y4]来处理，这就有结点来直接管了，也就是说对于[y1, y3]这种没有结点直接管的区间，也是能被拆成有限个区间被线段树的结点直接管辖的

这样做的好处是什么呢？就是为了解决上边的res怎么处理的问题，在这里每个结点的res的值都是独立的，所以处理起来也都是独立的，不存在要从父节点或子节点中获取的情况，而且这个len的处理也没有受到影响，依旧同上面那样的方式去维护即可

线段树构建好了，扫描线的扫法也知道了，那么我们接下来就只剩最后一步，就是把扫描线跟线段树揉和在一起，实际上这也很简单，扫描线当前覆盖了哪些边哪些信息，我们就把它们读入线段树即可

---

下面就贴AC代码了

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<vector>
using namespace std;

const int Maxn = ;

struct Edge {//平行于y轴的边
    double l, r;//边所覆盖区间
    double x;//边在x轴上的坐标
    int d;//该值为1或-1，表示入边或出边

    Edge(double l, double r, double x, int d) : l(l), r(r), x(x), d(d) {}

    bool operator < (const Edge& B) const {
        return x < B.x;
    }
};

struct Node { //线段树的结点
    int l, r; //结点所管辖区间
    int res; //区间被直接完全覆盖次数
    double len; //结点所管辖区间的有效覆盖长度
};

vector<double> x;
vector<double> y;

vector<Edge> e;
Node Tree[Maxn << ];

int getX(double X)
{
    return lower_bound(x.begin(), x.end(), X) - x.begin();
}

int getY(double Y)
{
    return lower_bound(y.begin(), y.end(), Y) - y.begin();
}

inline int lc(int p) {
    return p << ;
}

inline int rc(int p) {
    return p <<  | ;
}

void push_up(int p)
{
    if (Tree[p].res > ) Tree[p].len = Tree[p].len = y[Tree[p].r] - y[Tree[p].l]; //该区间线段已被直接覆盖，直接取其有效长度
    else if (Tree[p].l +  == Tree[p].r) Tree[p].len = ; //是叶子节点，则其有效长度为0
    else Tree[p].len = Tree[lc(p)].len + Tree[rc(p)].len;//不是被直接覆盖，就从子节点提取有效长度值
}

void Build_Tree(int l, int r, int p)
{
    Tree[p].l = l;
    Tree[p].r = r;

    if (l +  == r) return;

    int m = l + r >> ;
    Build_Tree(l, m, lc(p));
    Build_Tree(m, r, rc(p));
}

void update(int L, int R, int p, int d)
{
    if (Tree[p].r <= L || Tree[p].l >= R) return;
    if (L <= Tree[p].l && Tree[p].r <= R) {
        Tree[p].res += d;
        push_up(p);
        return;
    }

    update(L, R, lc(p), d);
    update(L, R, rc(p), d);
    push_up(p);
}

double Query()
{
    return Tree[].len;
}

void Test()
{
    for (int i = ; i < y.size(); i++) {
        printf("%d: %f\n", i, y[i]);
    }
}

void Ini()
{
    e.clear();
    x.clear();
    y.clear();
    memset(Tree, , sizeof(Tree));
}

void Input(int n)
{
    x.push_back(-); //使离散化的下标从1开始，喜欢从0开始的同学可以忽略
    y.push_back(-);
    for (int i = ; i <= n; i++) {
        double x1, y1, x2, y2;
        cin >> x1 >> y1 >> x2 >> y2;
        x.push_back(x1);
        x.push_back(x2);
        y.push_back(y1);
        y.push_back(y2);

        e.push_back(Edge(y1, y2, x1, ));
        e.push_back(Edge(y1, y2, x2, -));
    }
    e.push_back(Edge(, ,  + , ));//末尾添加个0值边，方便循环处理
}

void solve(int Case)
{
    cout << "Test case #" << Case << endl;
    sort(x.begin(), x.end());
    sort(y.begin(), y.end());
    sort(e.begin(), e.end());

    x.erase(unique(x.begin(), x.end()), x.end());
    y.erase(unique(y.begin(), y.end()), y.end());

    Build_Tree(, y.size() - , );

    double ans = ;
    int cur = ;
    for (int i = ; i < x.size()-; i++) {
        while (e[cur].x == x[i]) {
            update(getY(e[cur].l), getY(e[cur].r), , e[cur].d);
            cur++;
        }

        ans += Query() * (x[i + ] - x[i]);
    }

    printf("Total explored area: %.2f\n", ans);
}

int main()
{
    int Case = ;
    int n;
    while (cin >> n && n) {
        Case++;
        Ini();
        Input(n);
        solve(Case);
        cout << endl;
    }

    return ;
}