Leetcode883.Projection Area of 3D Shapes三维形体投影面积

在 N * N 的网格中，我们放置了一些与 x，y，z 三轴对齐的 1 * 1 * 1 立方体。

每个值 v = grid[i][j] 表示 v 个正方体叠放在单元格 (i, j) 上。

现在，我们查看这些立方体在 xy、yz 和 zx 平面上的投影。

投影就像影子，将三维形体映射到一个二维平面上。

在这里，从顶部、前面和侧面看立方体时，我们会看到“影子”。

返回所有三个投影的总面积。

示例 1：

输入：[[2]] 输出：5

示例 2：

输入：[[1,2],[3,4]] 输出：17 解释： 这里有该形体在三个轴对齐平面上的三个投影(“阴影部分”)。

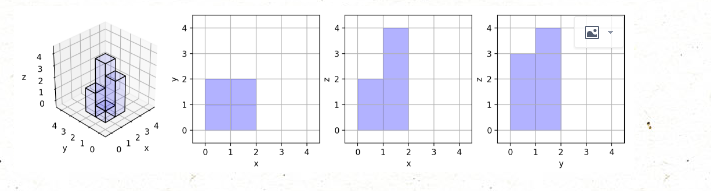
示例 3：

输入：[[1,0],[0,2]] 输出：8

示例 4：

输入：[[1,1,1],[1,0,1],[1,1,1]] 输出：14

示例 5：

输入：[[2,2,2],[2,1,2],[2,2,2]] 输出：21

提示：

• 1 <= grid.length = grid[0].length <= 50
• 0 <= grid[i][j] <= 50

投影在xy平面上，表示与z轴无关，

投影在yz平面上，表示与x轴无关

投影在xz平面上，表示与y轴无关

class Solution {
public:
    int projectionArea(vector<vector<int> >& grid)
    {
        int xy = 0;
        int r = grid.size();
        int c = grid[0].size();
        map<int, int> xz;
        map<int, int> yz;
        for(int i = 0; i < r; i++)
        {
            for(int j = 0; j < c; j++)
            {
                if(grid[i][j] > 0)
                {
                    xy++;
                    if(xz[i] != 0)
                    {
                        xz[i] = max(grid[i][j], xz[i]);
                    }
                    else
                    {
                        xz[i] = grid[i][j];
                    }
                    if(yz[j] != 0)
                    {
                        yz[j] = max(grid[i][j], yz[j]);
                    }
                    else
                    {
                        yz[j] = grid[i][j];
                    }
                }
            }
        }
        int sum = xy;
        for(map<int, int> :: iterator itr = xz.begin(); itr != xz.end(); itr++)
        {
            sum += itr ->second;
        }
        for(map<int, int> :: iterator itr = yz.begin(); itr != yz.end(); itr++)
        {
            sum += itr ->second;
        }
        return sum;
    }
};