ACM-ICPC Beijing 2016 Genius ACM（倍增+二分）

描述

给定一个整数 M，对于任意一个整数集合 S，定义“校验值”如下:

从集合 S 中取出 M 对数(即 2∗M 个数，不能重复使用集合中的数，如果 S 中的整数不够 M 对，则取到不能取为止)，使得“每对数的差的平方”之和最大，这个最大值就称为集合 S 的“校验值”。

现在给定一个长度为 N 的数列 A 以及一个整数 T。我们要把 A 分成若干段，使得每一段的“校验值”都不超过 T。求最少需要分成几段。

Advanced CPU Manufacturer (ACM) is one of the best CPU manufacturer in the world. Every day, they manufacture n CPU chips and sell them all over the world.

As you may know, each batch of CPU chips must pass a quality test by the QC department before they can be sold. The testing procedure is as follows:

1) Randomly pick m pairs of CPU chips from the batch of chips (If there are less than 2m CPU chips in the batch of chips, pick as many pairs as possible.)

2) For each pair, measure the Relative Performance Difference (RPD) between the two CPU chips. Let Di be the RPD of the i-th pair

3) Calculate the Sqared Performance Difference (SPD) of the batch according to the following formula:

SPD=∑Di2

If there are only 1 CPU in a batch, then the SPD of that batch is 0.

4) The batch of chips pass the test if and only if SPD≤k, where k is a preseted constant

Usually they send all the n CPU chips as a single batch to the QC department every day. As one of the best CPU manufacturer in the world, ACM never fail the test. However, with the continuous improvement of CPU performance, they find that they are at risk!

Of course they don't want to take any risks. So they make a decision to divide the n chips into several batches to ensure all of them pass the test. What’s more, each batch should be a continuous subsequence of their productions, otherwise the QC department will notice that they are cheating. Quality tests need time and money, so they want to minimize the number of batches.

Given the absolute performance of the n chips P1 ... Pn mesured by ACM in order of manufacture, your task is to determine the minimum number of batches to ensure that all chips pass the test. The RPD of two CPU chips equals to the difference of their absolute performance.

输入格式

The first line contains a single integer T, indicating the number of test cases.

In each test case, the first line contains three integers n, m, k. The second line contains n integers, P1 ... Pn.

输出格式

For each test case, print the answer in a single line.

样例输入

样例输出

2

1

数据范围与约定

T≤12
1≤n,m≤5e5
0≤k≤1e18
0≤Pi≤2e20

思路：

我们知道max（sum） = （最大-最小）²+（次大-次小）²+....

①暴力枚举，枚举每个sum <= T的最大位置， Σ（ilogi） ≈ O（n²logn）

②二分如果每次都只是向右扩展一位，那么二分的复杂度将会比枚举要高 O（n²log²n）

③倍增+二分我们让其快速增长，过头后，快速下降。 (倍增+二分 logn、排序校验nlogn) O（nlog²n）

我们让L = R = P = 1，先校验【L，R+P】，然后倍增R=R+P，P*=2；不符合要求就P/=2，直至P=0，L=R，就是sum <= T最大位置

那么每次符合倍增的时候【L，R】是上次校验过的，也就是说是有序的，我们只需要【R，R+P】排序，和前一段合并成【L，R+P】。

这样的复杂度是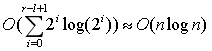

 #include<bits/stdc++.h>

 using namespace std;

 const int maxn = 5e5+;

 int t;

 int n,m;

 int L,R,p;

 typedef long long ll;

 ll k;

 ll num[maxn];

 ll tmpnum[maxn];

 ll tmpnum2[maxn];

 void Mergesort(int l,int mid,int r)

 {

     int i=l,j=mid+;

     int k = l;

     while(i <= mid && j <= r)

     {

         if(tmpnum2[i]<tmpnum2[j])

             tmpnum[k++] = tmpnum2[i++];

         else

             tmpnum[k++] = tmpnum2[j++];

     }

     while(i <= mid)

         tmpnum[k++] = tmpnum2[i++];

     while(j <= r)

         tmpnum[k++] = tmpnum2[j++];

 }

 bool Merge(int l,int mid,int r,int p)

 {

     for(int i=l; i<=r; i++)

         tmpnum2[i] = num[i];

     sort(tmpnum2+mid+,tmpnum2+r+);

     Mergesort(l,mid,r);

     int len = (l+r)/;

     ll tmp = ;

     for(int i=l; i<=len&&i < l+m; i++)

     {

         tmp += (tmpnum[l+r-i] - tmpnum[i])*(tmpnum[l+r-i] - tmpnum[i]);

     }

     if(tmp > k)

         return ;

     else

     {

         for(int i=l; i<=r; i++)

         {

             num[i] = tmpnum[i];

         }

         return ;

     }

 }

 int main()

 {

     scanf("%d",&t);

     while(t--)

     {

         scanf("%d%d%lld",&n,&m,&k);

         for(int i=; i<=n; i++)

             scanf("%lld",&num[i]);

         p=,R=,L=;

         int sum = ;

         while(R <= n)

         {

             if(p)

             {

                 if(R+p > n || Merge(L,R,R+p,p))

                     p/=;

                 else

                     R+=p,p *= ;

             }

             else

             {

                 R++;

                 L=R;

                 p++;

                 sum++;

             }

         }

         printf("%d\n",sum);

     }

 }