Deep Learning Tutorial - Classifying MNIST digits using Logistic Regression

Deep Learning Tutorial 由 Montreal大学的LISA实验室所作，基于Theano的深度学习材料.Theano是一个python库，使得写深度模型更容易些，也可以在GPU上训练深度模型。所以首先得了解python和numpy。其次，阅读Theano basic tutorial。

Deep Learning Tutorial 包括：

监督学习算法：

Logistic Regression - using Theano for something simple

Multilayer perceptron - introduction to layers

Deep Convolutional Network - a simplified version of LeNet5

无监督和半监督学习算法：

Auto Encoders, Denoising Autoencoders - description of autoencoders

Stacked Denoising Auto-Encoders - easy steps into unsupervised pre-training for deep nets

Restricted Boltzmann Machines - single layer generative RBM model

            Deep Belief Networks - unsupervised generative pre-training of stacked RBMs followed by supervised fine-tuning
        建立mcRBM模型：
             HMC Sampling

        其他：

Contractive auto-encoders：

Semantic Parsing of Speech using Recurrent Net

              LSTM network

              Modeling and generating sequences of polyphonic music

1.Getting started：

      存储数据时用shared variables（共享变量），用小批量索引来操作数据。共享变量与利用GPU有关，如果数据时共享变量，Theano可以复制整个数据在GPU上通过一个简单的命令，不需要从CPU存储上复制任何信息。当在GPU上存储数据时需要的类型是floats，因此代码type为floatX。由于y为标签，所以要将y cast为int。

2.损失函数：

0-1损失：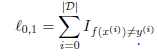  

对数似然损失：，因为0-1损失函数不可微，我们一般用最大化对数似然损失，即最小化负的对     数似然损失。

3.梯度下降

批梯度、随机梯度、小批量梯度

4.正则化

L1，L2正则化（权重衰减）

5.提前停止（Early-Stopping）

之前没注意这个算法，后面的logistic回归分类手写数字识别时用到了它。思想大致是：在验证数据集上如果连续多次迭代过程中损失函数不再显著降低，那么应该提前结束训练，同时也可防止过拟合。

6.Theano tips

若要存储在程序运行过程后所优化得到的权重参数，利用pickle或深拷贝，如果参数为共享变量w,v,u，可这样操作：

>>> import cPickle
>>> save_file = open(’path’, ’wb’) # this will overwrite current contents
>>> cPickle.dump(w.get_value(borrow=True), save_file, -1) # the -1 is for HIGHEST_PROTOCOL
>>> cPickle.dump(v.get_value(borrow=True), save_file, -1) # .. and it triggers much more efficient
>>> cPickle.dump(u.get_value(borrow=True), save_file, -1) # .. storage than numpy’s default
>>> save_file.close()

若要用这些w,v,u来预测或评价，可以再load一下：

>>> save_file = open(’path’)
>>> w.set_value(cPickle.load(save_file), borrow=True)
>>> v.set_value(cPickle.load(save_file), borrow=True)
>>> u.set_value(cPickle.load(save_file), borrow=True)

建议不要pickle训练或测试函数为长期储存，Theano函数与python深拷贝和pickle机制兼容，如果你更新了Theano文件使其内部改变，那么可能将无法在un-pickle你的模型。

CLASSIFYING MNIST DIGITS USING LOGISTIC REGRESSION

logistic regression模型（打分or评价函数）：

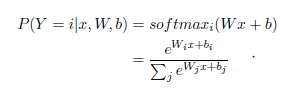
logistic regression模型（损失函数）：

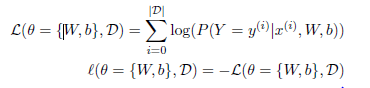
整体代码：

#coding=UTF-8
import cPickle
import gzip
import os
import sys
import timeit
import numpy
import theano
import theano.tensor as T

class LogisticRegression(object):   #此类有三个函数
    def __init__(self, input, n_in, n_out):
        self.W = theano.shared(value=numpy.zeros((n_in, n_out), dtype=theano.config.floatX),name='W',borrow=True)  #初始化参数
        self.b = theano.shared(value=numpy.zeros((n_out,), dtype=theano.config.floatX), name='b', borrow=True)
        self.p_y_given_x = T.nnet.softmax(T.dot(input, self.W) + self.b)   #计算打分、评价结果
        self.y_pred = T.argmax(self.p_y_given_x, axis=1)      #挑出可能性最大的类别标签
        self.params = [self.W, self.b]
        self.input = input

    def negative_log_likelihood(self, y):
        return -T.mean(T.log(self.p_y_given_x)[T.arange(y.shape[0]), y])    #计算损失函数

    def errors(self, y):        #计算错误率
        if y.ndim != self.y_pred.ndim:
            raise TypeError('y should have the same shape as self.y_pred', ('y', y.type, 'y_pred', self.y_pred.type))
        if y.dtype.startswith('int'):
            return T.mean(T.neq(self.y_pred, y))
        else:
            raise NotImplementedError()

def load_data(dataset):
    f = gzip.open(dataset,'rb')
    train_set, valid_set, test_set = cPickle.load(f)
    f.close()    #下载数据

    def shared_dataset(data_xy, borrow=True):   #将数据类型改为共享数据类型
        data_x, data_y = data_xy
        shared_x = theano.shared(numpy.asarray(data_x, dtype=theano.config.floatX), borrow=borrow)
        shared_y = theano.shared(numpy.asarray(data_y, dtype=theano.config.floatX), borrow=borrow)
        return shared_x, T.cast(shared_y, 'int32')

    test_set_x, test_set_y = shared_dataset(test_set)
    valid_set_x, valid_set_y = shared_dataset(valid_set)
    train_set_x, train_set_y = shared_dataset(train_set)
    rval = [(train_set_x, train_set_y), (valid_set_x, valid_set_y), (test_set_x, test_set_y)]   #改好的三种共享数据类型
    return rval

def sgd_optimization_mnist(learning_rate=0.13, n_epochs=1000, dataset='data/mnist.pkl.gz', batch_size=600):   #随机梯度下降
    datasets = load_data(dataset)                     #学习速率0.13，迭代次数1000，批梯度大小600
    train_set_x, train_set_y = datasets[0]
    valid_set_x, valid_set_y = datasets[1]
    test_set_x, test_set_y = datasets[2]
    n_train_batches = train_set_x.get_value(borrow=True).shape[0] / batch_size
    n_valid_batches = valid_set_x.get_value(borrow=True).shape[0] / batch_size
    n_test_batches = test_set_x.get_value(borrow=True).shape[0] / batch_size        #计算三种数据的批量数目，若train_set有6000个样本，批梯度大小为600，
    print '...building the model'                                                   #则n_train_batches为10.
    index = T.lscalar()
    x = T.matrix('x')
    y = T.ivector('y')
    classifier = LogisticRegression(input=x, n_in=28 * 28, n_out=10)    #Classifer为这个分类器
    cost = classifier.negative_log_likelihood(y)
    test_model = theano.function(     #测试模型
        inputs=[index],
        outputs=classifier.errors(y),
        givens={
            x: test_set_x[index * batch_size: (index + 1) * batch_size],
            y: test_set_y[index * batch_size: (index + 1) * batch_size]
        }
    )
    validate_model = theano.function(   #验证模型
        inputs=[index],
        outputs=classifier.errors(y),    #输出为错误率
        givens={
            x: valid_set_x[index * batch_size: (index + 1) * batch_size],
            y: valid_set_y[index * batch_size: (index + 1) * batch_size]
        }
    )
    g_W = T.grad(cost=cost, wrt=classifier.W)
    g_b = T.grad(cost=cost, wrt=classifier.b)
    updates = [(classifier.W, classifier.W - learning_rate * g_W), (classifier.b, classifier.b - learning_rate * g_b)]
    train_model = theano.function(    #训练模型
        inputs=[index],
        outputs=cost,
        updates=updates,
        givens={
            x: train_set_x[index * batch_size: (index + 1) * batch_size],
            y: train_set_y[index * batch_size: (index + 1) * batch_size]
        }
    )
    print '...training the model'          #以下运用了early-stop算法，并非普通的迭代n次后停止
    patience = 5000
    patience_increase = 2
    improvement_threshold = 0.995
    validation_frequency = min(n_train_batches, patience / 2)
    best_validation_loss = numpy.inf
    test_score = 0.
    start_time = timeit.default_timer()
    done_looping = False
    epoch = 0
    while (epoch < n_epochs) and (not done_looping):    #设置最大迭代次数n_epochs
        epoch = epoch + 1
        for minibatch_index in xrange(n_train_batches):     #小批量梯度，实际中n_train)batches=83
            minibatch_avg_cost = train_model(minibatch_index)
            iter = (epoch - 1) * n_train_batches + minibatch_index    #minibatch_index最大只能取到82
            if (iter + 1) % validation_frequency == 0:         #满足这个条件说明完整的迭代了一个epoch，即将所有训练样本迭代了一次
                validation_losses = [validate_model(i) for i in xrange(n_valid_batches)]
                this_validation_loss = numpy.mean(validation_losses)   #计算验证集错误率
                print('epoch %i, minibatch %i / %i, validation error %f %%' %(epoch, minibatch_index + 1, n_train_batches, this_validation_loss * 100.))
                if this_validation_loss < best_validation_loss:     #如果找到了优者
                    if this_validation_loss < best_validation_loss * improvement_threshold:  #如果找到了优者*0.995（即很吊的优者）
                        patience = max(patience, iter * patience_increase)   #遇到了更吊的优者就更新参数
                    best_validation_loss = this_validation_loss    #不论屌不屌，只要找到优者就存起来
                    test_losses = [test_model(i) for i in xrange(n_test_batches)]
                    test_score = numpy.mean(test_losses)    #计算测试集的错误率
                    print(('epoch %i, minibatch %i / %i, test error of'' best model %f %%') %(epoch,minibatch_index + 1,n_train_batches,test_score * 100.))
                    with open('best_model.pkl', 'w') as f:cPickle.dump(classifier, f)    #存储已跑完的训练模型结果！
            if patience <= iter:   #当满足这个条件跳出迭代！
                done_looping = True
                break
    end_time = timeit.default_timer()
    print(('Optimization complete with best validation score of %f %%,''with test performance %f %%') %(best_validation_loss*100.,test_score*100.))
    print 'The code run for %d epochs,with %f epochs/esc' % (epoch, 1.*epoch/(end_time-start_time))

def predict():
    classifier = cPickle.load(open('best_model.pkl'))   #调出已存好了的训练模型！
    predict_model = theano.function(inputs=[classifier.input], outputs=classifier.y_pr ed)  #预测模型
    dataset = 'data/mnist.pkl.gz'
    datasets = load_data(dataset)
    test_set_x, test_set_y = datasets[2]
    test_set_x = test_set_x.get_value()      #取出其值
    #test_set_y = test_set_y
    predicted_values = predict_model(test_set_x[:10])        #取出前10个预测下
    print("predicted values for the first 10 examples in test set:")
    print predicted_values