HDU 6397 Character Encoding (组合数学 + 容斥)

题意：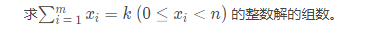

析：首先很容易可以看出来使用FFT是能够做的，但是时间上一定会TLE的，可以使用公式化简，最后能够化简到最简单的模式。

其实考虑使用组合数学，如果这个 xi 没有限制，那么就是求 x1 + x2 + x3 +... xm = k，有多少非零解，隔板法很容易得到答案 C(k+m-1, m-1)，但是有限制怎么办，使用容斥，考虑有一个变量超过 n-1，两个变量超过 n-1，等等，根据集合论，很容易知道偶加，奇减。。。

代码如下：

#pragma comment(linker, "/STACK:1024000000,1024000000")
#include <cstdio>
#include <string>
#include <cstdlib>
#include <cmath>
#include <iostream>
#include <cstring>
#include <set>
#include <queue>
#include <algorithm>
#include <vector>
#include <map>
#include <cctype>
#include <cmath>
#include <stack>
#include <sstream>
#include <list>
#include <assert.h>
#include <bitset>
#include <numeric>
#define debug() puts("++++")
#define gcd(a, b) __gcd(a, b)
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
#define fi first
#define se second
#define pb push_back
#define sqr(x) ((x)*(x))
#define ms(a,b) memset(a, b, sizeof a)
#define sz size()
#define be begin()
#define ed end()
#define pu push_up
#define pd push_down
#define cl clear()
#define lowbit(x) -x&x
// #define all 1,n,1
#define FOR(i,n,x)  for(int i = (x); i < (n); ++i)
#define freopenr freopen("in.in", "r", stdin)
#define freopenw freopen("out.out", "w", stdout)
using namespace std;

typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int, int> P;
const int INF = 0x3f3f3f3f;
const LL LNF = 1e17;
const double inf = 1e20;
const double PI = acos(-1.0);
const double eps = 1e-8;
const int maxn = 200000 + 10;
const int maxm = 1e6 + 10;
const LL mod = 998244353LL;
const int dr[] = {-1, 1, 0, 0, 1, 1, -1, -1};
const int dc[] = {0, 0, 1, -1, 1, -1, 1, -1};
const char *de[] = {"0000", "0001", "0010", "0011", "0100", "0101", "0110", "0111", "1000", "1001", "1010", "1011", "1100", "1101", "1110", "1111"};
int n, m;
const int mon[] = {0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
const int monn[] = {0, 31, 29, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
inline bool is_in(int r, int c) {
  return r >= 0 && r < n && c >= 0 && c < m;
}
inline int readInt(){ int x;  scanf("%d", &x);  return x; }

LL fact[maxn], inv[maxn];

LL fast_pow(LL a, int n){
  LL res = 1;
  while(n){
    if(n&1)  res = res * a % mod;
    n >>= 1;
    a = a * a % mod;
  }
  return res;
}

void init(){
  fact[0] = fact[1] = 1;
  for(int i = 2; i < maxn; ++i)  fact[i] = fact[i-1] * i % mod;
  inv[maxn-1] = fast_pow(fact[maxn-1], mod - 2);
  for(int i = maxn-2; i >= 0; --i)  inv[i] = inv[i+1] * (i+1) % mod;
}

inline LL C(int n, int m){
  if(n < m)  return 0LL;
  return fact[n] * inv[m] % mod * inv[n-m] % mod;
}

inline LL G(int x, int k){
  return C(m, x) * C(k - x * n + m - 1, m - 1) % mod;
}

int main(){
  init();
  int T, k;  cin >> T;
  while(T--){
    scanf("%d %d %d", &n, &m, &k);
    if(n > k){ printf("%I64d\n", C(m+k-1, m-1));  continue; }
    LL ans = 0;
    for(int i = 0; i <= (k + m - 1) / n; ++i)
      ans = (ans + (i&1? -G(i, k) : G(i, k))) % mod;
    printf("%I64d\n", (ans%mod+mod)%mod);
  }
  return 0;
}