P1403 [AHOI2005]约数研究

原题链接 https://www.luogu.org/problemnew/show/P1403

这个好难啊，求约数和一般的套路就是求1--n所有的约数再一一求和，求约数又要用for循环来判断......恩～～......貌似很简单，看一下n的范围：100%N<=1000000......额，看来要炸

那么怎么办呢?这时候我们就要用玄学啦当然要耐心枚举几个数找找规律啦！

从洛谷题解里看到一位大佬的约数表，再看他详细的解释，终于明白了这个题的玄学所在，放约数图！！！

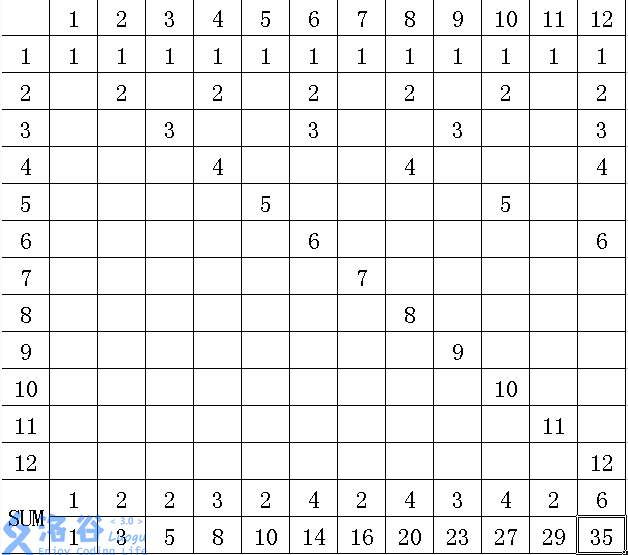
我们通过这个表可以发现： 在1--n这n个数中有n/1个数是1的倍数，有n/2个数是2的倍数，有n/3个数是3的倍数........有n个数是n的倍数（c++中‘/’会省略小数取整型）

所以问题的解就是n/1+n/2+n/3+.......+n/n

代码如下：

#include<iostream>
#include<cstdio>
#include<math.h>
using namespace std;
int n,sum=;
int main()
{
int n,sum=;
cin>>n;
for(int i=;i<=n;i++)
sum+=n/i;
cout<<sum;
return ;
}