二分搜索-HihoCoder1139

题目描述：

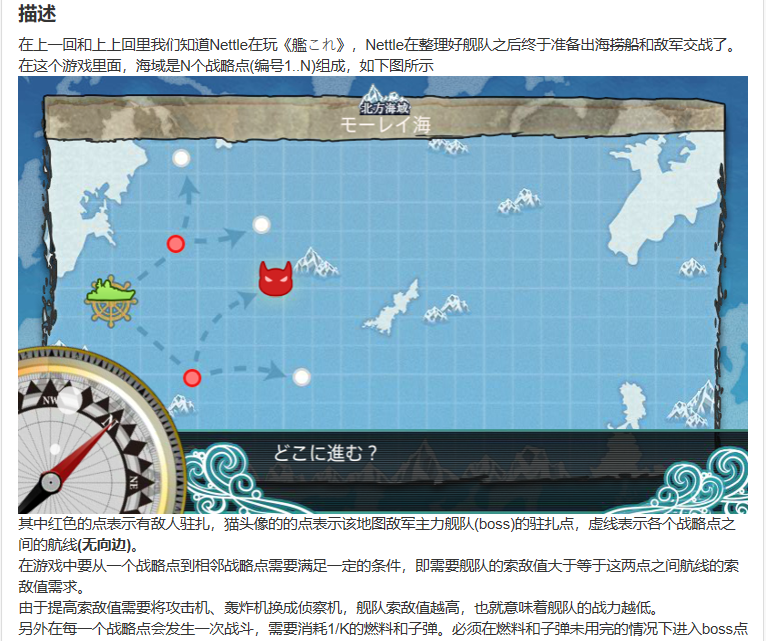
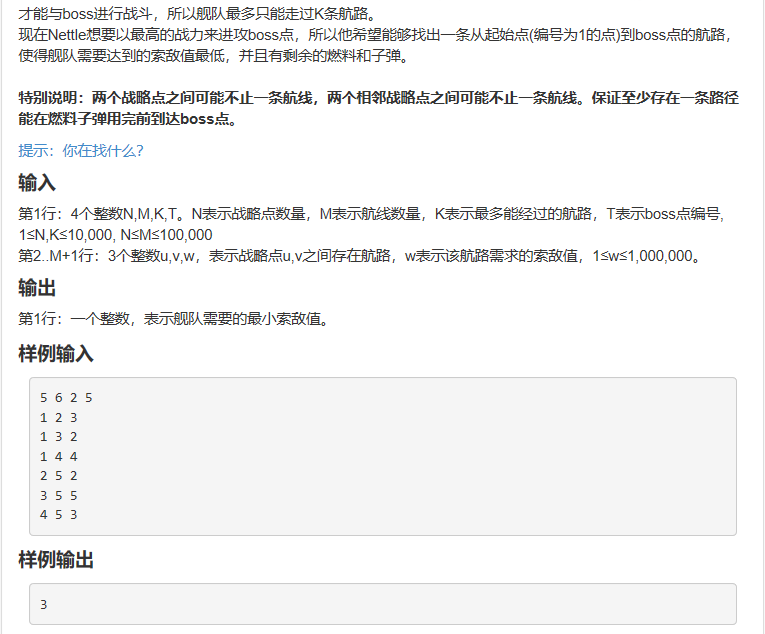
由于自己“想得太多”，导致自己读了半天题才理解了题意。我还以为索敌值会随着每一次到达战略点而减小，结果题意是索敌值是固定了的，并不会改变。

如下是我对题目中第一个案例的分析：

每个圆圈代表一个战略点的编号，边上的值代表每两个战略点之间所需索敌值。

　　　　　　　　　　　　　　    

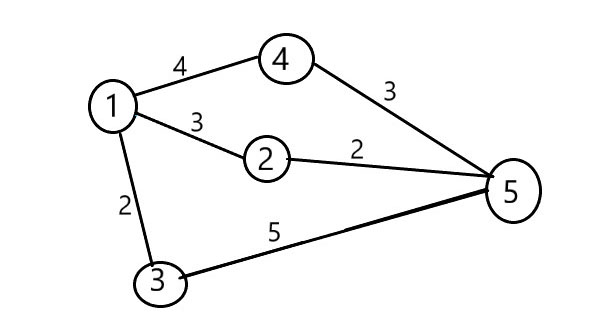
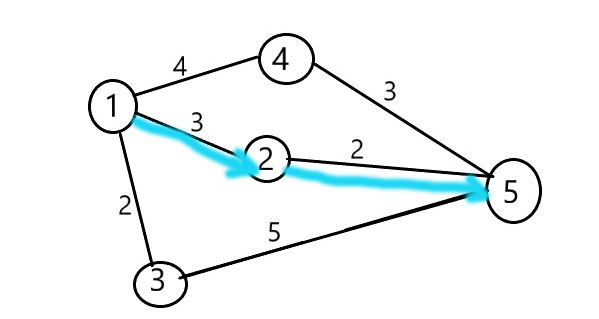
开始时Nettle在1，他只需要3个索敌值就能到达5了，如图：从战略点1到达战略点5只需要 3 个索敌值，因此答案 3 满足条件，再从战略点2到战略点5只需要 2 个索敌值，答案3大于2，因此答案 3 满足条件。所以，Nettle需要的最少索敌值为3，经1---->2---->5路线，可以消灭boss。

代码实现：

#include <cstdio>
#include <vector>
#include <cstring>
#include <queue>
#include <algorithm>
using namespace std;
const int MAXN = 1e6;
const int INF = +;
int N,M,K,T;
struct edge{
    int from;//源点
    int to;//目标点
    int val;//锁敌值
};

struct node{
    int to;//目标点
    int val;//锁敌值
};
edge E[MAXN*];///所有的边
edge now[MAXN*];///满足k>=val的边
vector<node> G[MAXN];///满足k>=val的边对应的点
bool used[MAXN];
typedef pair<int,int> P;
queue<P> q;
int cmp(edge a, edge b){
    return a.val<b.val;//从小到大排序
}

bool bfs(int num,int k){///广搜从1到BOSS点的路径
    while(!q.empty()){
        q.pop();
    }
    q.push(P(num,k));
    used[num]=true;
    while(!q.empty()){
        P top = q.front();
        q.pop();
        if(top.first==T){
            return true;
        }
        for(int i=;i<G[top.first].size();i++){
            if(!used[G[top.first][i].to]){
                used[G[top.first][i].to]=true;
                if(top.second>0){///保证索敌值始终大于零，一直广搜总会找到一个合适的索敌值
                    q.push(P(G[top.first][i].to,top.second-));///每次执行后使索敌值-1
                }
            }
        }
    }
    return false;
}

bool C(int x){
    int cnt=;
    memset(used,,sizeof(used));
    for(int i=;i<MAXN;i++){
        G[i].clear();///满足val>=k的边对应的点
    }
    ///满足锁敌值为x的边存在now数组里面
    for(int i=;i<*M;i++){
        if(E[i].val<=x){///如果这条边的索敌值比答案x的索敌值小，就放入now数组里面
            now[cnt++]=E[i];
        }
    }
    for(int i=;i<cnt;i++){
        G[now[i].from].push_back((node){now[i].to,now[i].val});
    }
    if(bfs(,K)){///广搜从1到BOSS点的路径
        return true;
    }
    return false;
}

void solve(){
    int lb=,ub=INF;
    while(ub-lb>){
        int mid=(ub+lb)/;
        ///满足锁敌值为x，且能够找到1点到BOSS点的路径
        if(C(mid)){
            ub=mid;
        }else{
            lb=mid;
        }
    }
    printf("%d\n",ub);

}

int main(){
    while(~scanf("%d%d%d%d",&N,&M,&K,&T)){
        for(int i=;i<M;i++){
            int a,b,val;
            scanf("%d%d%d",&a,&b,&val);
            E[i].from=a;E[i].to=b;E[i].val=val;///记录每条边的起始和所需索敌值
            E[i+M].from=b;E[i+M].to=a;E[i+M].val=val;///将其存为有向图
        }
        sort(E,E+*M,cmp);
        solve();
    }
    return ;
}