dp入门 石子相邻合并 详细带图讲解

题目：

有N堆石子，现要将石子有序的合并成一堆，规定如下：

1.每次只能移动相邻的2堆石子合并 
2.合并花费为新合成的一堆石子的数量。

求将这N堆石子合并成一堆的总花费最小（或最大）。

样例：

输入：7

13 7 8 16 21 4 18

输出：239

说是简单dp，刚开始学dp还是有点困难，这个题目我花了很长时间了。今天差不多才理清里面的大部分细节。

首先，合并相邻的石子，合并时，可以两堆，三堆，四堆。两堆的时候就只能合并相邻两堆；三堆的时候就有多种选择了，1+2 和 2+1；四堆的时候，1+3 和 2+2 和 3+1；

2堆的时候：

3堆的时候：

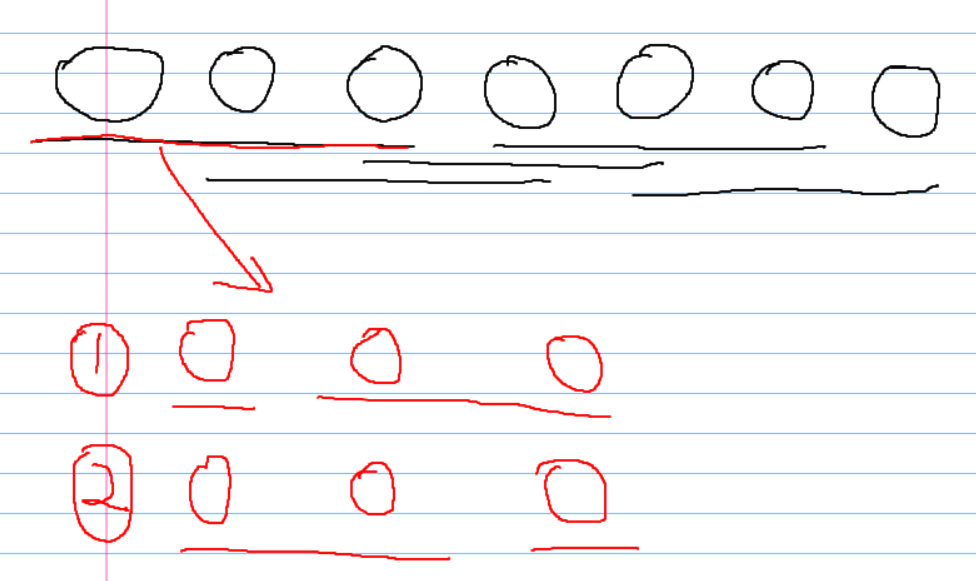
4堆也是类似。

现在我们拿样例来分析一下。

1.首先是状态转移方程。

设f[i][j]是从第i堆到第j堆的最优值。  配和上面的图，两堆的时候：f[1][2] f[2][3] f[3][4] f[4][5] f[5][6] f[6][7]; 三堆的时候：f[1][3] f[2][4] ......。

然后 f[1][3] = f[1][1] + f[2][3] + s[3] - s[0];    f[1][3] = f[1][2] + f[3][3] + s[3] - s[0];  有这两种情况。取他们的最小值。

转移方程就是 f[i][j] = min( f[i][j], f[i][k] + f[k+1][j] +s[j]-s[i]);

2.为什么是s[3] - s[0]呢？

s[3] - s[0]是从第1堆到第3堆的总和。但是花销并不仅仅是总和， 合并3堆的时候，其实是需要合并两次，所以每堆都用到了两次，而自己和自己合并，花费的价值为0。f[1][3] = f[1][1] + f[2][3] + s[3] - s[0]； f[1][1] + f[2][3]这个是一次合并，s[3] - s[0]这个是另外一次合并。

3.输出的答案是f[1][n]。

代表从第1堆到第n堆的最小花费。

4.为什么要倒推？

因为顺推的时候，f[1][3] = f[2][3] + f[1][1] ，顺推的话，i从1开始，那f[2][3]这个时候是没办法知道的。所以倒推。

代码：

#include<bits/stdc++.h>
using namespace std;
const int M = 10009;

int f[M][M]; // f[i][j] 代表第 i 堆石子 到 第 j 堆石子的最优值
int x,s[M]; 

int main(){
	int n;
	cin>>n;
	memset(f,1011/3,sizeof(f));
	for(int i = 1; i <= n; i++)
	{
		cin>>x;
		s[i] = s[i-1] + x; //s[i] 代表前 i 堆石子的总和
	}

	for(int i = 1; i <= n; i++) f[i][i] = 0;

	for(int i = n-1; i >= 1; i--)
		for(int j = i+1; j <= n; j++)
			for(int k = i; k <= j-1; k++)
			{
				f[i][j] = min(f[i][j],f[i][k]+f[k+1][j]+s[j]-s[i-1]);
			}

	cout<<f[1][n];

	return 0;
}