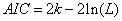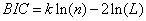aic bic mdl
https://blog.csdn.net/xianlingmao/article/details/7891277
https://blog.csdn.net/lfdanding/article/details/50732762
参考文章http://blog.csdn.net/lynnucas/article/details/47947943
转自:http://blog.csdn.net/jteng/article/details/40823675
此处模型选择我们只考虑模型参数数量,不涉及模型结构的选择。
很多参数估计问题均采用似然函数作为目标函数,当训练数据足够多时,可以不断提高模型精度,但是以提高模型复杂度为代价的,同时带来一个机器学习中非常普遍的问题——过拟合。所以,模型选择问题在模型复杂度与模型对数据集描述能力(即似然函数)之间寻求最佳平衡。
人们提出许多信息准则,通过加入模型复杂度的惩罚项来避免过拟合问题,此处我们介绍一下常用的两个模型选择方法——赤池信息准则(Akaike Information Criterion,AIC)和贝叶斯信息准则(Bayesian Information Criterion,BIC)。
AIC是衡量统计模型拟合优良性的一种标准,由日本统计学家赤池弘次在1974年提出,它建立在熵的概念上,提供了权衡估计模型复杂度和拟合数据优良性的标准。
通常情况下,AIC定义为:
其中k是模型参数个数,L是似然函数。从一组可供选择的模型中选择最佳模型时,通常选择AIC最小的模型。
当两个模型之间存在较大差异时,差异主要体现在似然函数项,当似然函数差异不显著时,上式第一项,即模型复杂度则起作用,从而参数个数少的模型是较好的选择。
一般而言,当模型复杂度提高(k增大)时,似然函数L也会增大,从而使AIC变小,但是k过大时,似然函数增速减缓,导致AIC增大,模型过于复杂容易造成过拟合现象。目标是选取AIC最小的模型,AIC不仅要提高模型拟合度(极大似然),而且引入了惩罚项,使模型参数尽可能少,有助于降低过拟合的可能性。
BIC(Bayesian InformationCriterion)贝叶斯信息准则与AIC相似,用于模型选择,1978年由Schwarz提出。训练模型时,增加参数数量,也就是增加模型复杂度,会增大似然函数,但是也会导致过拟合现象,针对该问题,AIC和BIC均引入了与模型参数个数相关的惩罚项,BIC的惩罚项比AIC的大,考虑了样本数量,样本数量过多时,可有效防止模型精度过高造成的模型复杂度过高。
其中,k为模型参数个数,n为样本数量,L为似然函数。kln(n)惩罚项在维数过大且训练样本数据相对较少的情况下,可以有效避免出现维度灾难现象。
经常地,对一堆数据进行建模的时候,特别是分类和回归模型,我们有很多的变量可供使用,选择不同的变量组合可以得到不同的模型,例如我们有5个变量,2的5次方,我们将有32个变量组合,可以训练出32个模型。但是哪个模型更加的好呢?目前常用有如下方法:
AIC=-2 ln(L) + 2 k 中文名字:赤池信息量 akaike information criterion
BIC=-2 ln(L) + ln(n)*k 中文名字:贝叶斯信息量 bayesian information criterion
HQ=-2 ln(L) + ln(ln(n))*k hannan-quinn criterion
其中L是在该模型下的最大似然,n是数据数量,k是模型的变量个数。
注意这些规则只是刻画了用某个模型之后相对“真实模型”的信息损失【因为不知道真正的模型是什么样子,所以训练得到的所有模型都只是真实模型的一个近似模型】,所以用这些规则不能说明某个模型的精确度,即三个模型A, B, C,在通过这些规则计算后,我们知道B模型是三个模型中最好的,但是不能保证B这个模型就能够很好地刻画数据,因为很有可能这三个模型都是非常糟糕的,B只是烂苹果中的相对好的苹果而已。
这些规则理论上是比较漂亮的,但是实际在模型选择中应用起来还是有些困难的,例如上面我们说了5个变量就有32个变量组合,如果是10个变量呢?2的10次方,我们不可能对所有这些模型进行一一验证AIC, BIC,HQ规则来选择模型,工作量太大。
aic bic mdl的更多相关文章
- PRML学习笔记第一章
[转] PRML笔记 - 1.1介绍 模式识别的目标 自动从数据中发现潜在规律,以利用这些规律做后续操作,如数据分类等. 模型选择和参数调节 类似的一族规律通常可以以一种模型的形式为表达,选择合适模型 ...
- Introduction to Writing Functions in R
目录 在R中编写函数 args(函数名) 创建一个函数的步骤 1.default args Passing arguments between functions Checking arguments ...
- 7 Types of Regression Techniques you should know!
翻译来自:http://news.csdn.net/article_preview.html?preview=1&reload=1&arcid=2825492 摘要:本文解释了回归分析 ...
- geoR文档翻译
说来惭愧,很久没有更新自己的博客了.期间个人生活经历了很多变故,心理上的打击尤甚.加之没有取得好的科研成果,痛定思痛,还是下苦功夫多多学习. 最近对比验证各种方法的插值精度,用到了R语言地统计学包,由 ...
- 【机器学习笔记之五】用ARIMA模型做需求预测用ARIMA模型做需求预测
本文结构: 时间序列分析? 什么是ARIMA? ARIMA数学模型? input,output 是什么? 怎么用?-代码实例 常见问题? 时间序列分析? 时间序列,就是按时间顺序排列的,随时间变化的数 ...
- python时间序列分析
题记:毕业一年多天天coding,好久没写paper了.在这动荡的日子里,也希望写点东西让自己静一静.恰好前段时间用python做了一点时间序列方面的东西,有一丁点心得体会想和大家 ...
- 时间序列算法(平稳时间序列模型,AR(p),MA(q),ARMA(p,q)模型和非平稳时间序列模型,ARIMA(p,d,q)模型)的模型以及需要的概念基础学习笔记梳理
在做很多与时间序列有关的预测时,比如股票预测,餐厅菜品销量预测时常常会用到时间序列算法,之前在学习这方面的知识时发现这方面的知识讲解不多,所以自己对时间序列算法中的常用概念和模型进行梳理总结(但是为了 ...
- 使用RStudio调试(debug)基础学习(二)和fGarch包中的garchFit函数估计GARCH模型的原理和源码
一.garchFit函数的参数--------------------------------------------- algorithm a string parameter that deter ...
- Python机器学习——线性模型
http://www.dataguru.cn/portal.php?mod=view&aid=3514 摘要 : 最近断断续续地在接触一些python的东西.按照我的习惯,首先从应用层面搞起, ...
随机推荐
- LeetCode 977 Squares of a Sorted Array 解题报告
题目要求 Given an array of integers A sorted in non-decreasing order, return an array of the squares of ...
- 自定义指令(v-check、v-focus)的方法有哪些?它有哪些钩子函数?还有哪些钩子函数参数?
全局定义指令:在vue对象的directive方法里面有两个参数,一个是指令名称,另一个是函数.组件内定义指令:directives: 钩子函数:bind(绑定事件触发).inserted(节点插入的 ...
- JVM java垃圾回收机制
一.jvm简介 1.JVM内存运行时数据区的三个重要的地方 1.1.堆(heap):它是最大的一块区域,用于存放对象实例数组,是全局共享的. 1.2.栈(stack):全称为虚拟机栈,主要存储基本数据 ...
- 前端 HTML form表单标签 input标签 type属性 重置按钮 reset
input type="reset" value="重置" reset重置 还原到默认状态 <!DOCTYPE html> <html lan ...
- python实时得到鼠标的位置
1.#先下载pyautogui库,打开cmd输入pip install pyautogui,回车 2.代码如下: import os,time import pyautogui as pag try: ...
- 帝国cms-tab
<ul class="intro_commenTab"> [e:loop={"select classname,classpath,classid from ...
- golang 中处理大规模tcp socket网络连接的方法,相当于c语言的 poll 或 epoll
https://groups.google.com/forum/#!topic/golang-nuts/I7a_3B8_9Gw https://groups.google.com/forum/#!ms ...
- QGL登陆wui 提示not possible
1: sap 登陆 QGL系统, 提示 2: 需要到该系统下,使用 T-CODE su01 或者 su3 对LIHANS1 用户角色进行修改. 3:su53 查询 自己操作的 历史纪录和 状 ...
- Vue+typescript报错项
39:1 Unable to resolve signature of class decorator when called as an expression. Type '<VC exten ...
- 【LeetCode每天一题】Trapping Rain Water(获得雨水的容量)
Given n non-negative integers representing an elevation map where the width of each bar is 1, comput ...