APIO2014 连珠线

题目链接：戳我

换根DP

由于蒟蒻不会做这个题，所以参考了大佬。

本来想的是有三种情况，一种是该节点不作为两个蓝线的中点（我们称这种不是关键节点），一种是该节点作为关键点、连两个子节点，一种是作为关键节点、一个连子节点一个连父亲节点。

然后有一个不换根的树形DP，但是正确性emmm尚待商榷。

对于一个这样的图——

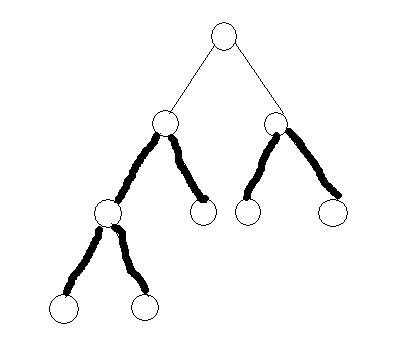
我们可以发现，如果想要连起来的话，我们需要不止一个根节点，而这与题目中提到的每次加入一个节点不符。

所以我们考虑换根。这样的话我们发现，就只有两种情况了——一种是该节点不作为关键节点，一种是作为关键节点、连父亲和儿子。

设\(f[i][0]\)表示对于以i为根的子树，该节点不作为关键节点的最大收益。

设\(f[i][1]\)表示对于以i为根的子树，该节点作为关键节点、连父节点和子节点的最大收益。

\(f[i][0]=max(f[i][0],f[i][1]+edge[i].dis)\)

\(f[i][1]=max(f[i][1],f[i][0]-max(dp[v][0],dp[v][1]+dis)+dis+dp[v][0])\)

之后维护一个\((f[i][0]-max(dp[v][0],dp[v][1]+dis)+dis+dp[v][0])\)的前后缀即可。

具体看代码qwqwq

代码如下：

#include<iostream>
#include<cstring>
#include<cstdio>
#include<vector>
#include<algorithm>
#define MAXN 200010
#define INF 0x3f3f3f3f
using namespace std;
int n,t,ans;
int head[MAXN],f[MAXN][2];
vector<int>son[MAXN],pef[MAXN],suf[MAXN],dis[MAXN];
struct Edge{int nxt,to,dis;}edge[MAXN<<1];
inline void add(int from,int to,int dis)
{
    edge[++t].nxt=head[from],edge[t].to=to,edge[t].dis=dis,head[from]=t;
    edge[++t].nxt=head[to],edge[t].to=from,edge[t].dis=dis,head[to]=t;
}
inline int dfs1(int x,int pre)
{
    f[x][0]=0,f[x][1]=-INF;
    for(int i=head[x];i;i=edge[i].nxt)
    {
        int v=edge[i].to;
        if(v==pre) continue;
        son[x].push_back(v),dis[x].push_back(edge[i].dis);
    }
    for(int i=0;i<son[x].size();i++)
    {
        int v=son[x][i],dist=dis[x][i];
        dfs1(v,x);
        f[x][0]+=max(f[v][0],f[v][1]+dist);
        pef[x].push_back(f[v][0]-max(f[v][0],f[v][1]+dist)+dist);
        suf[x].push_back(f[v][0]-max(f[v][0],f[v][1]+dist)+dist);
    }
    for(int i=0;i<son[x].size();i++) f[x][1]=max(f[x][1],f[x][0]+pef[x][i]);
    for(int i=1;i<son[x].size();i++) pef[x][i]=max(pef[x][i],pef[x][i-1]);
    for(int i=son[x].size()-2;i>=0;i--) suf[x][i]=max(suf[x][i],suf[x][i+1]);
}
inline void dfs2(int x,int f0,int f1,int dist)
{
    f[x][0]+=max(f0,f1+dist);
    f[x][1]+=max(f0,f1+dist);
    f[x][1]=max(f[x][1],f[x][0]+f0-max(f0,f1+dist)+dist);
    ans=max(ans,f[x][0]);
    for(int i=0;i<son[x].size();i++)
    {
        int v=son[x][i];
        int cur0=f[x][0]-max(f[v][0],f[v][1]+dis[x][i]);
        int delta=f0-max(f0,f1+dist)+dist;
        if(i!=0) delta=max(delta,pef[x][i-1]);
        if(i!=son[x].size()-1) delta=max(delta,suf[x][i+1]);
        dfs2(v,cur0,cur0+delta,dis[x][i]);
    }
}
int main()
{
    #ifndef ONLINE_JUDGE
    freopen("ce.in","r",stdin);
    #endif
    scanf("%d",&n);
    for(int i=1;i<n;i++)
    {
        int u,v,w;
        scanf("%d%d%d",&u,&v,&w);
        add(u,v,w);
    }
    dfs1(1,0);
    dfs2(1,0,-INF,-INF);
    printf("%d\n",ans);
    return 0;
}