洛谷 P1466 集合 Subset Sums Label：DP

题目描述

对于从1到N (1 <= N <= 39) 的连续整数集合，能划分成两个子集合，且保证每个集合的数字和是相等的。举个例子，如果N=3，对于{1，2，3}能划分成两个子集合，每个子集合的所有数字和是相等的：

{3} 和 {1,2}

这是唯一一种分法（交换集合位置被认为是同一种划分方案，因此不会增加划分方案总数） 如果N=7，有四种方法能划分集合{1，2，3，4，5，6，7}，每一种分法的子集合各数字和是相等的:

{1,6,7} 和 {2,3,4,5} {注 1+6+7=2+3+4+5}
{2,5,7} 和 {1,3,4,6}
{3,4,7} 和 {1,2,5,6}
{1,2,4,7} 和 {3,5,6}
给出N，你的程序应该输出划分方案总数，如果不存在这样的划分方案，则输出0。程序不能预存结果直接输出（不能打表）。

输入输出格式

输入格式：

输入文件只有一行，且只有一个整数N

输出格式：

输出划分方案总数，如果不存在则输出0。

输入输出样例

输入样例#1：

7

输出样例#1：

4

说明

翻译来自NOCOW

USACO 2.2

代码

 #include<iostream>
 #include<algorithm>
 #include<cstring>
 #include<cstdio>
 #include<cstdlib>
 #include<cmath>
 using namespace std;

 int f[][];//f[i][j]表示i分成两组差为j的分法
 int N;

 int main(){
 //    freopen("01.in","r",stdin);
     scanf("%d",&N);
     f[][]=f[][]=;f[][]=;
     for(int i=;i<=N;i++){
         for(int j=;j<=(i*(i+)/);j++){
             if(j+i<=(i*(i+)/))        f[i][j]+=f[i-][j+i];
             if(j>=i)                    f[i][j]+=f[i-][j-i];
             if(j!=)                      f[i][j]+=f[i-][i-j];
         }
     }

     printf("%d",f[N][]);
     fclose(stdin);fclose(stdout);return ;
 }

很明显这是一道DP，自己思考一下Line 18 19 20吧

转载另外一种解法：

---

题解by:redbag

原题解地址：http://redbag.duapp.com/?p=1197

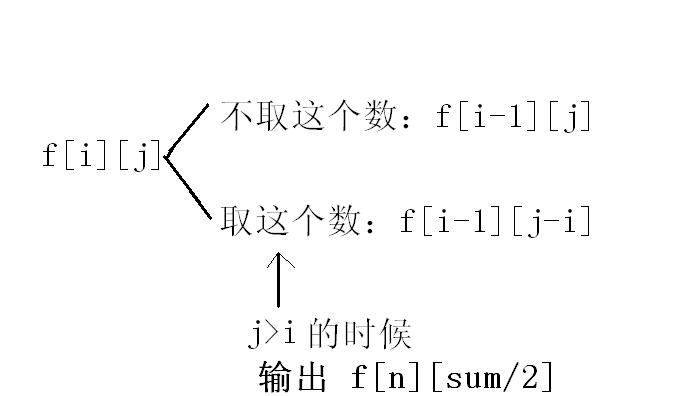
n个数的总和为sum:=n*(n+1)shr 1,当且仅当sum为偶数的时候才有解，sum为奇数时直接输出0并且退出程序；然后每个数只有2种情况，放在第一个集合和不放在第一个集合。于是就是简单的01背包问题了。简单的分析见图

 #include<set>
 #include<map>
 #include<list>
 #include<queue>
 #include<stack>
 #include<string>
 #include<math.h>
 #include<time.h>
 #include<vector>
 #include<bitset>
 #include<memory>
 #include<utility>
 #include<stdio.h>
 #include<sstream>
 #include<iostream>
 #include<stdlib.h>
 #include<string.h>
 #include<algorithm>
 #define LL unsigned long long
 using namespace std;
 int sum/*1~n的和*/,n;
 int f[][];
 int i,j;
 int main()
 {
     freopen("subset.in","r",stdin);
     freopen("subset.out","w",stdout);
     scanf("%d",&n);
     sum=(n*(n+))/;//算出1~n的和。
     if (sum%==)//仅当sum为偶数的时候才有解
     {
         printf("0\n");//因为分成的2份和要相等
         return ;
     }
     f[][]=;//1中取任意个数的数使和为1的情况
     f[][]=;//1中取任意个数的数使和为0的情况
     for (i=;i<=n;i++)//1的情况已经算完了，所以从2开始
     {
         for (j=;j<=sum;j++)
         {
             if (j>i)//有取这个数和不取两种情况
                 f[i][j]=f[i-][j]+f[i-][j-i];
                 else f[i][j]=f[i-][j];//只能不取了
         }
     }
     printf("%d\n",f[n][sum/]);
     return ;
 }

原来这只是一个辣么简单的背包，我想得。。。。。。。也太复杂了吧