HDU - 5017 Ellipsoid(模拟退火法)

Problem Description

Given a 3-dimension ellipsoid(椭球面)




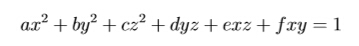
your task is to find the minimal distance between the original point (0,0,0) and points on the ellipsoid. The distance between two points (x₁,y₁,z₁) and (x₂,y₂,z₂) is defined as 

 

Input

There are multiple test cases. Please process till EOF.



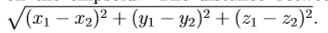
For each testcase, one line contains 6 real number a,b,c(0 < a,b,c,< 1),d,e,f(0 ≤ d,e,f < 1), as described above. It is guaranteed that the input data forms a ellipsoid. All numbers are fit in double.

 

Output

For each test contains one line. Describes the minimal distance. Answer will be considered as correct if their absolute error is less than 10^-5.

 

Sample Input

1 0.04 0.01 0 0 0

 

Sample Output

1.0000000

 

Source

2014 ACM/ICPC Asia Regional Xi'an Online

题意：求椭圆上离圆心近期的点的距离。

思路：模拟退火法，学着网上写的

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
const int inf = 1e8;
const double eps = 1e-8;

const int dx[8] = {0,0,1,-1,1,-1,1,-1};
const int dy[8] = {1,-1,0,0,1,1,-1,-1};
double a, b, c, d, e, f;

double dis(double x, double y, double z) {
	return sqrt(x * x + y * y + z * z);
}

double calz(double x, double y) {
	double A = c;
	double B = d * y + e * x;
	double C = f * x * y + a * x * x + b * y * y - 1.0;
	double delta = B * B - 4.0 * A * C;

	if (delta < 0.0) return inf+10.0;
	delta = sqrt(delta);
	double z1 = (-B + delta) / (2.0 * A);
	double z2 = (-B - delta) / (2.0 * A);
	if (dis(x, y, z1) < dis(x, y, z2))
		return z1;
	return z2;
}

double solve() {
	double x = 0, y = 0, z = sqrt(1.0/c);
	double step = 1.0, rate = 0.99;
	while (step > eps) {
		for (int k = 0; k < 8; k++) {
			double nx = x + step * dx[k];
			double ny = y + step * dy[k];
			double nz = calz(nx, ny);

			if (nz >= inf) continue;
			if (dis(nx, ny, nz) < dis(x, y, z)) {
				x = nx;
				y = ny;
				z = nz;
			}
		}
		step *= rate;
	}
	return dis(x, y, z);
}

int main() {
	while (scanf("%lf%lf%lf%lf%lf%lf", &a, &b, &c, &d, &e, &f) != EOF) {
		printf("%.7lf\n", solve());
	}
	return 0;
}