【bzoj1001】[BeiJing2006]狼抓兔子 最小割+对偶图+最短路

题目描述

现在小朋友们最喜欢的"喜羊羊与灰太狼",话说灰太狼抓羊不到，但抓兔子还是比较在行的，而且现在的兔子还比较笨，它们只有两个窝，现在你做为狼王，面对下面这样一个网格的地形：

左上角点为(1,1),右下角点为(N,M)(上图中N=4,M=5).有以下三种类型的道路 

1:(x,y)<==>(x+1,y) 

2:(x,y)<==>(x,y+1) 

3:(x,y)<==>(x+1,y+1) 

道路上的权值表示这条路上最多能够通过的兔子数，道路是无向的. 左上角和右下角为兔子的两个窝，开始时所有的兔子都聚集在左上角(1,1)的窝里，现在它们要跑到右下解(N,M)的窝中去，狼王开始伏击这些兔子.当然为了保险起见，如果一条道路上最多通过的兔子数为K，狼王需要安排同样数量的K只狼，才能完全封锁这条道路，你需要帮助狼王安排一个伏击方案，使得在将兔子一网打尽的前提下，参与的狼的数量要最小。因为狼还要去找喜羊羊麻烦.

输入

第一行为N,M.表示网格的大小，N,M均小于等于1000.

接下来分三部分

第一部分共N行，每行M-1个数，表示横向道路的权值. 

第二部分共N-1行，每行M个数，表示纵向道路的权值. 

第三部分共N-1行，每行M-1个数，表示斜向道路的权值. 

输入文件保证不超过10M

输出

输出一个整数，表示参与伏击的狼的最小数量.

样例输入

3 4
5 6 4
4 3 1
7 5 3
5 6 7 8
8 7 6 5
5 5 5
6 6 6

样例输出

14

---

题解

最小割，转化成对偶图最短路来求。

由于点数边数都很大，直接跑最大流肯定会TLE。

想到题目中图有特殊规律，方便转化为对偶图。

于是可以先转化为对偶图，再求最短路。

步骤：

1.连一条s->t的边

2.为图中每个面积块标号，方法自己选择，s->t边内侧为(s')，外侧为(t')（反过来也一样，因为无向图）

3.连接题目中每条边挨着的两个面积块，权值为原边权，注意要连无向边。

效果：

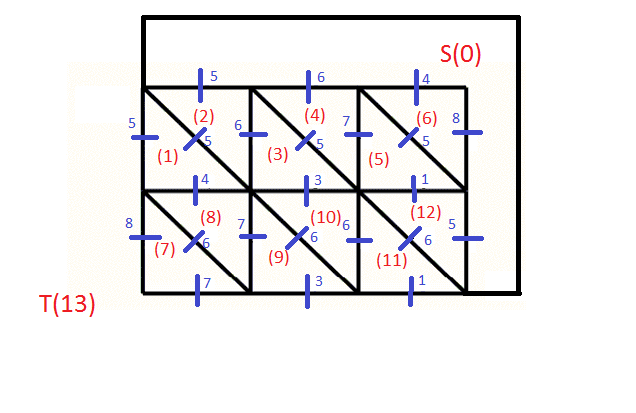
其中黑色为原图边，红色为新点，蓝色为新边，蓝色数字为新边权。

看似很麻烦，点边很多，实际上堆优化Dijkstra很快，而Dinic慢到死。

然后跑堆优化Dijkstra即可。

#include <cstdio>
#include <cstring>
#include <utility>
#include <queue>
using namespace std;
priority_queue<pair<int , int> > q;
int head[2000010] , to[6000010] , len[6000010] , next[6000010] , cnt , dis[2000010] , vis[2000010];
void add(int x , int y , int z)
{
	to[++cnt] = y;
	len[cnt] = z;
	next[cnt] = head[x];
	head[x] = cnt;
}
int main()
{
	int n , m , i , j , x , y , z , s , t;
	scanf("%d%d" , &n , &m);
	s = 0 , t = (n - 1) * (m - 1) * 2 + 1;
	for(i = 1 ; i <= n ; i ++ )
	{
		for(j = 1 ; j < m ; j ++ )
		{
			scanf("%d" , &z);
			if(i == 1) x = s; else x = (i - 2) * (m - 1) * 2 + (j - 1) * 2 + 1;
			if(i == n) y = t; else y = (i - 1) * (m - 1) * 2 + (j - 1) * 2 + 2;
			add(x , y , z) , add(y , x , z);
		}
	}
	for(i = 1 ; i < n ; i ++ )
	{
		for(j = 1 ; j <= m ; j ++ )
		{
			scanf("%d" , &z);
			if(j == 1) x = t; else x = (i - 1) * (m - 1) * 2 + (j - 2) * 2 + 2;
			if(j == m) y = s; else y = (i - 1) * (m - 1) * 2 + (j - 1) * 2 + 1;
			add(x , y , z) , add(y , x , z);
		}
	}
	for(i = 1 ; i < n ; i ++ )
	{
		for(j = 1 ; j < m ; j ++ )
		{
			scanf("%d" , &z);
			x = (i - 1) * (m - 1) * 2 + (j - 1) * 2 + 1;
			y = (i - 1) * (m - 1) * 2 + (j - 1) * 2 + 2;
			add(x , y , z) , add(y , x , z);
		}
	}
	memset(dis , 0x3f , sizeof(dis));
	dis[s] = 0;
	q.push(make_pair(0 , s));
	while(!q.empty())
	{
		x = q.top().second , q.pop();
		if(vis[x]) continue;
		vis[x] = 1;
		for(i = head[x] ; i ; i = next[i])
			if(dis[to[i]] > dis[x] + len[i])
				dis[to[i]] = dis[x] + len[i] , q.push(make_pair(-dis[to[i]] , to[i]));
	}
	printf("%d\n" , dis[t]);
	return 0;
}