萌新也能看懂的KMP算法

前言

算法是什么?算法就是数学规律.怎么去总结和发现这个规律,就是理解算法的过程.

KMP算法的本质是穷举法,而并不是去创造新的匹配逻辑.

以下将搜寻的字符串称为子串(part),以P表示.被搜寻的字符串称为总串(total),以T表示.

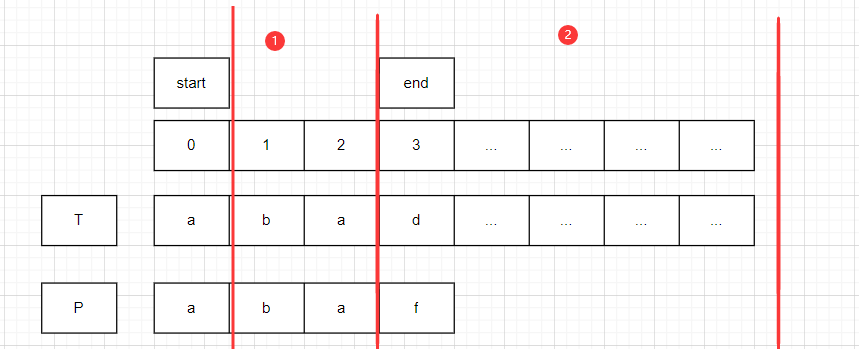
start代表P串在T串中开始匹配的位置,end代表P串与T串对比字符时的位置

        String total = "ababcd";
        String part = "abc";
        total.contains(part);

部分匹配表

部分匹配表是KMP算法的核心。只要理解了部分匹配表,就基本理解了KMP算法。

普通匹配模式

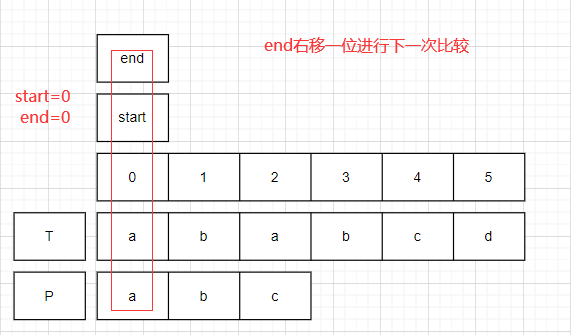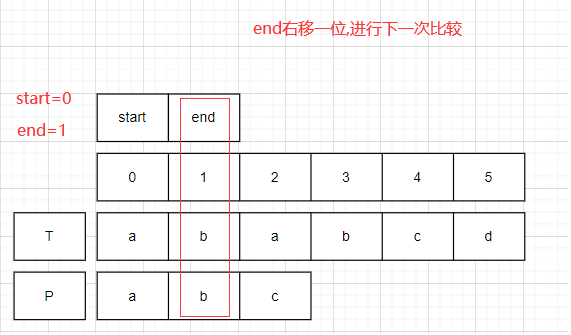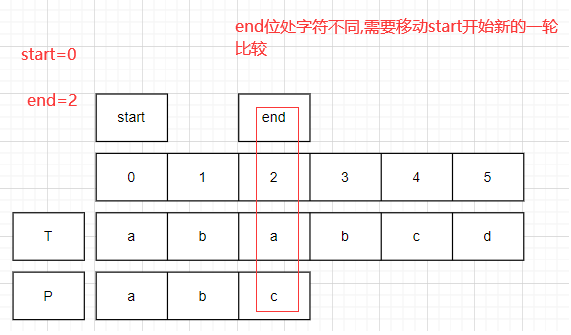
对比开始.

start=0,end=0;比较T.charAt(0)==P.charAt(0).均为a,此时end右移一位.

start=0,end=1;比较T.charAt(1)==P.charAt(1).均为b,此时end右移一位.

start=0,end=2;比较T.charAt(2)!=P.charAt(2).此时,start右移一位.

start=1,end=0;比较T.charAt(start+end)!=P.charAt(end).此时,start右移一位.

start=2,end=0;比较T.charAt(start+end)==P.charAt(end).此时,此时end右移一位.以此类推.

最终发现T.contains(P)为true,T.indexOf(P)为start,即为2.

    public static int getIndex(String total, String part) {
        char[] totalChars = total.toCharArray();
        char[] partChars = part.toCharArray();
        int start = 0;
        int end = 0;

        while (start < total.length()) {
            if (totalChars[start + end] == partChars[end]) {
                end++;
            } else {
                start = start + 1;
                end = 0;
            }
            if (end == part.length()) {
                return start;
            }
        }
        return -1;
    }

寻找规律

规律是什么?就是在匹配过程中,遇到某一位不匹配时.start与end下一次的起点位置选择.

对于普通匹配而言,start的变化永远是右移一位,end永远是从0开始,并且每次右移一位.

这里先介绍两个规律,当发现end位不匹配时

第一条规律,,新起点位置只与重合部分有关

T.charAt(start+end)!=P.charAt(end)

T.substring(start,start+end)==P.substring(0,end)

因为它不相等,所以它相等,这句话前后顺序不能颠倒.这虽然很像废话,但是确实KMP算法的核心.

第二条规律,未知无法跳过

这次的end位一定是下次比较的起点

这里有个特殊的地方,就是首位不同时的逻辑,代码中也是一样,先按下不表.

部分匹配表

有个比较关键的地方,确定start与end新起点的规则是什么?

---

新的起点是什么,是可能性,是T串的某一段与P串完全相同的可能性.

只有end=0时相同,才会有end=1时的比较

只有end=1时相同,才会有end=2时的比较

...

那么至少,T.charAt(start)==P.charAt(0),才可以进行后面的比较

---

当遇到end位不匹配时,我们将start可能移动的轨迹分为两部分

① (start,start+end)

② [start+end,...]

T.indexOf(P)的位置只可能出现在这两个区域(因为之前的位置都被排除了).这两个区域的差别是什么呢?

结合上面两条规律,途经区域①的比较的字符对象是完全已知的,而区域②则不是.

即下一次start的起点在 (start,start+end] 中

因为即要么在(start,start+end)中,要么就是end,因为end是未知的,必须要用首位去对比,所以start最远会位移到end位

由于第一条规律,T.substring(start,start+end)==P.substring(0,end)

那么start在T.substring(start,start+end)中位移的过程就是start在P.substring(0,end)中位移的过程

去寻找start在(start,start+end)中作为新起点的可能性,就是寻P.substring(0,end)这个字符串本身与其子串的重合度,什么是重合度?

两个相同的字符串,一个不动,一个整体向右移动一格,查看两者相交部分,如果相交部分完全相等,那么相交字符串的首位,就是新的起点,这个相交部分的长度就是重合度.

---

假设 P = abcde

不匹配时end位置	P.substring(0,end)	重合度
0	""	0
1	a	0
2	ab	0
3	abc	0
4	abcd	0

获取重合度

    public static int getPublicPart(String part) {
        int start = 1;
        int end = 0;
        char[] chars = part.toCharArray();
        while (start < part.length()) {
            if (chars[start + end] == chars[end]) {
                if (end + start == part.length() - 1) {
                    return part.substring(start).length();
                }
                end++;
            } else {
                start++;
                end = 0;
            }
        }
        return 0;
    }

我们将start移动轨迹的研究,变成了P.substring(0,end)的研究,那么假设T串很长,那么end值可能会出现在任意一个地方,并且相同情况会有多次,所以我们只要事先将所有可能的情况列出,以后遇到相同情况就可以直接套用结果.

为什么可以复用呢?因为P.charAt(end)我们一定知道什么,但是T.charAt(start+end)却有很多种可能,因为它只需要与P.charAt(end)不相等

---

假设 P = aaaab

不匹配时end位置	P.substring(0,end)	重合度	下一次start位置	下一次end位置
4	aaaa	3	start+4-3	3
3	aaa	2	start+3-2	2
2	aa	1	start+2-1	1
1	a	0	start+1-0	0
0	""	0	start+0-(-1)	0

我们可以发现,start下一次的位置为 start +（ end - P.substring(0,end)的重合度). (end - 重合度) 其实就是start需要位移的距离

---

end下一次的位置为 P.substring(0,end)的重合度

但是由于P.substring(0,0)为空字符串,比较特殊,首位不同时,start是直接右移一位

---

故令next[0] = -1 , 当 next[end] < 0时,下一次的end位置指向 0

获取next数组

    public static int[] getNext(String part) {
        int[] next = new int[part.length()];
        int start = 1;
        while (start < part.length()) {
            next[start] = getPublicPart(part.substring(0, start));
            start++;
        }
        next[0] = -1;
        return next;
    }

我们将end位不同时,P.substring(0,end)它的子串与自身的重合度,称之为部分匹配表

Tips:



这里有一个很关键的地方,start可以直接从0移动到2吗?不可以,因为KMP无法违背普通匹配,或者说违背匹配的规律,只有start每次右移一位,即P.charAt(0)与T串的每一位开始比较,才能确认这个位置含不含有可能性,而我们next数组的获取就是通过每次右移一位获取到的.

完整代码

KMP算法的本质就是通过穷举end位不匹配时start与end的移动轨迹,来达到复用的效果.

    public static int indexOf(String total, String part) {
        char[] totalChars = total.toCharArray();
        char[] partChars = part.toCharArray();
        int[] next = getNext(part);

        int start = 0;
        int end = 0;
        while (start < total.length()) {
            if (totalChars[start + end] == partChars[end]) {
                end++;
            } else {
                // 与普通匹配不同的其实就是end位不同时,下一次start与end的位置选择
                start = start + end - next[end];
                end = Math.max(0, next[end]);
            }
            if (end == part.length()) {
                return start;
            }
        }
        return -1;
    }

---

小小的一篇文章,写了快一个月,每天晚上将思想转化为文字时,总会有新的理解,修修改改了这么长时间,总觉得文字不够干练.人生亦是如此.