2022-09-05：作为国王的统治者，你有一支巫师军队听你指挥。 :给你一个下标从 0 开始的整数数组 strength ， 其中 strength[i] 表示第 i 位巫师的力量值。 对于连续的一

2022-09-05：作为国王的统治者，你有一支巫师军队听你指挥。
:给你一个下标从 0 开始的整数数组 strength ，
其中 strength[i] 表示第 i 位巫师的力量值。
对于连续的一组巫师（也就是这些巫师的力量值是 strength 的 子数组），
总力量 定义为以下两个值的 乘积 ：
巫师中 最弱 的能力值 * 组中所有巫师的个人力量值 之和 。
请你返回 所有 巫师组的 总 力量之和。由于答案可能很大，请将答案对 109 + 7 取余 后返回。
子数组 是一个数组里 非空 连续子序列。

答案2022-09-05：

单调栈。

代码用rust编写。代码如下：

fn main() {
    let mut arr = vec![1, 3, 1, 2];
    let ans = total_strength(&mut arr);
    println!("ans = {}", ans);
}

const mod0: i64 = 1000000007;

fn total_strength(arr: &mut Vec<i32>) -> i32 {
    let n = arr.len() as i32;
    let mut pre_sum = arr[0] as i64;
    let mut sum_sum: Vec<i64> = vec![];
    for _ in 0..n {
        sum_sum.push(0);
    }
    sum_sum[0] = arr[0] as i64;
    for i in 1..n {
        pre_sum += arr[i as usize] as i64;
        sum_sum[i as usize] = (sum_sum[(i - 1) as usize] + pre_sum) % mod0;
    }
    let mut stack: Vec<i32> = vec![];
    for _ in 0..n {
        stack.push(0);
    }
    let mut size: i32 = 0;
    let mut ans: i64 = 0;
    for i in 0..n {
        while size > 0 && arr[stack[(size - 1) as usize] as usize] >= arr[i as usize] {
            size -= 1;
            let m = stack[size as usize];
            let l = if size > 0 {
                stack[(size - 1) as usize]
            } else {
                -1
            };
            // l（<当前值，且最近，到不了）        m(当前数，做为最小值)      i(<=当前数，到不了的！)
            ans += magic_sum(arr, &mut sum_sum, l, m, i);
            ans %= mod0;
        }
        stack[size as usize] = i;
        size += 1;
    }
    while size > 0 {
        size -= 1;
        let m = stack[size as usize];
        let l = if size > 0 {
            stack[(size - 1) as usize]
        } else {
            -1
        };
        ans += magic_sum(arr, &mut sum_sum, l, m, n);
        ans %= mod0;
    }
    ans as i32
}

fn magic_sum(arr: &mut Vec<i32>, sum_sum: &mut Vec<i64>, l: i32, m: i32, r: i32) -> i64 {
    let left = (m as i64 - l as i64)
        * (sum_sum[(r - 1) as usize]
            - if m - 1 >= 0 {
                sum_sum[(m - 1) as usize]
            } else {
                0
            }
            + mod0)
        % mod0;
    let right = (r as i64 - m as i64)
        * (if m - 1 >= 0 {
            sum_sum[(m - 1) as usize]
        } else {
            0
        } - if l - 1 >= 0 {
            sum_sum[(l - 1) as usize]
        } else {
            0
        } + mod0)
        % mod0;
    return arr[m as usize] as i64 * ((left - right + mod0) % mod0);
}

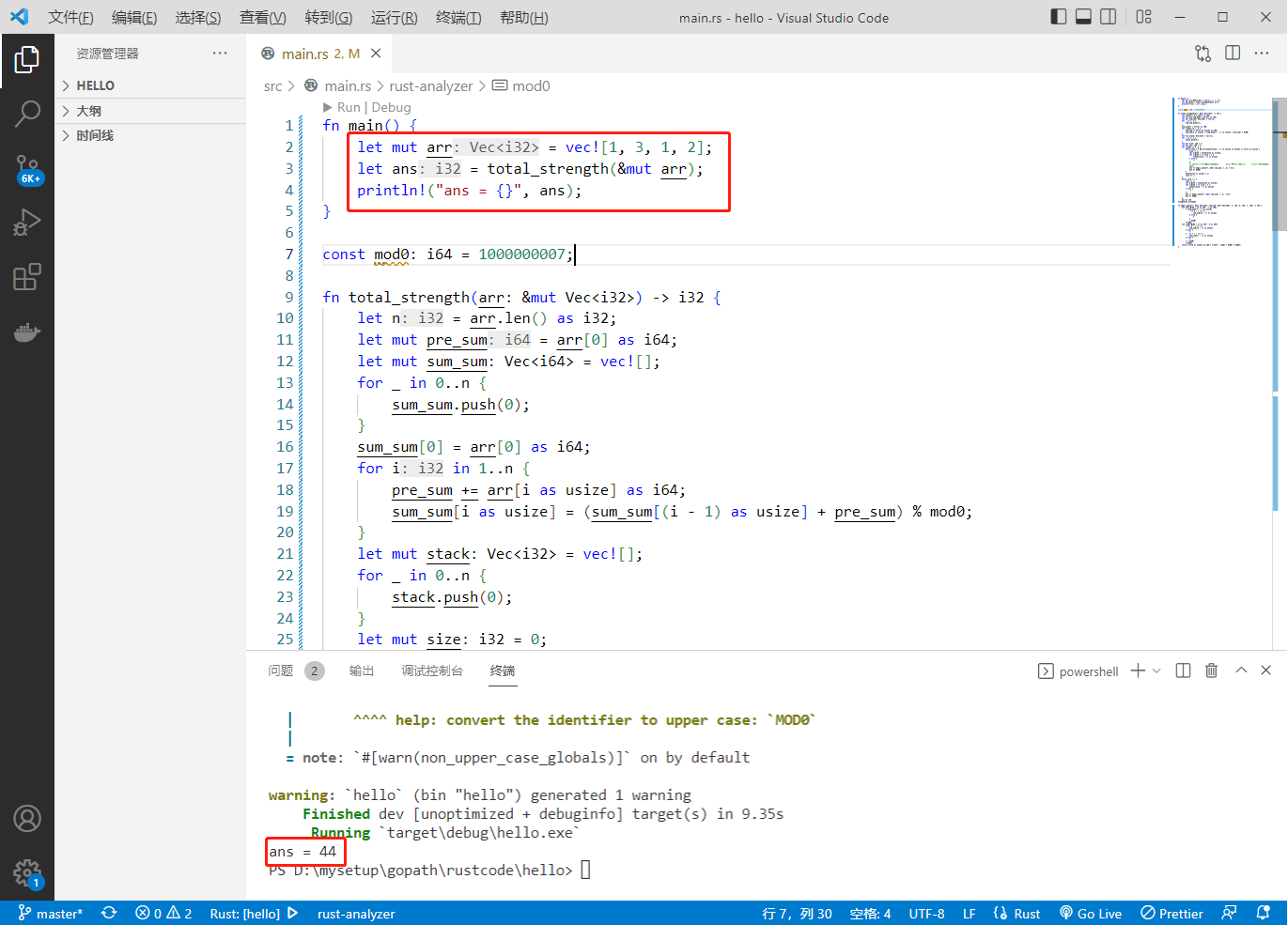
执行结果如下：

---

左神java代码