2023-03-22：给定一个字符串str， 如果删掉连续一段子串，剩下的字符串拼接起来是回文串， 那么该删除叫做有效的删除。 返回有多少种有效删除。 注意 : 不能全删除，删成空串不允许， 字符串长

2023-03-22：给定一个字符串str，
如果删掉连续一段子串，剩下的字符串拼接起来是回文串，
那么该删除叫做有效的删除。
返回有多少种有效删除。
注意 : 不能全删除，删成空串不允许，
字符串长度 <= 3000。

答案2023-03-22：

解法1：暴力枚举

算法思路

暴力枚举法即将所有可能的子串都枚举出来，并判断其是否是回文串。

具体实现

首先，我们来看如何判断一个字符串是否是回文串。我们可以使用双指针法，即左右指针分别指向字符串的头部和尾部，然后向中间扫描，逐个比较对应位置上的字符。若对应位置上的字符不相等，则该字符串不是回文串；否则，该字符串是回文串。

接着，我们来考虑如何枚举所有的子串。我们可以使用两层循环遍历字符串s，第一层循环变量i从0到n-1，第二层循环变量j从i到n-1。在每次循环中，我们都将s[0:i]和s[j+1:n-1]拼接起来得到新的字符串，然后再判断该字符串是否是回文串，如果是，则计数器ans加1。

但是，我们还需要排除掉空字符串和单个字符的情况，因此最终答案要减去1。

rust代码实现

fn good1(str: &str) -> i32 {
    let n = str.len();
    let mut ans = 0;
    for i in 0..n {
        for j in i..n {
            if is_palindrome(&(str[0..i].to_owned() + &str[j + 1..])) {
                ans += 1;
            }
        }
    }
    return ans - 1;
}

fn is_palindrome(str: &str) -> bool {
    let bytes = str.as_bytes();
    let mut l = 0;
    let mut r = bytes.len() as i32 - 1;

    while l <= r {
        if bytes[l as usize] != bytes[r as usize] {
            return false;
        }
        l += 1;
        r -= 1;
    }
    return true;
}

算法复杂度

时间复杂度：O( n ^ 3 )，其中n是字符串的长度。需要枚举O(n ^ 2)个子串，每个子串需要O(n)的时间判断是否是回文串。

空间复杂度：O(1)。只需要常数级别的空间存储变量。

解法2：Manacher算法

算法思路

Manacher算法是专门用于求解回文子串问题的经典算法。思想是利用已经求解出的回文子串来推导新的回文子串，从而减少重复计算。具体来说，它维护一个当前已知的最长回文半径，以及对应的回文中心。然后，按照顺序依次遍历字符串，对于每个位置，用已知的信息来快速计算出以该位置为中心的回文子串。由于每个位置只会被遍历一次，因此时间复杂度可以做到线性。

具体实现

Manacher算法需要对字符串进行预处理，将其转换为一个新的字符串。具体来说，我们在每个字符的左右插入一个特殊字符（例如#），然后在字符串开头和结尾分别插入另一个特殊字符（例如^和$）。这样做的目的是将所有回文子串都统一成奇数长度，方便后续计算。

接着，我们维护两个变量，分别表示当前已知的最长回文半径和对应的回文中心。对于每个位置i，我们首先利用已知信息计算出以i为中心的回文半径p[i]，然后更新最长回文半径和对应的回文中心。最后，我们将p[i]存储到一个数组中，在遍历完整个字符串之后，遍历该数组，计算出所有回文子串的个数。

具体实现时，为了方便计算，我们可以使用两个变量c和r来维护当前已知的最长回文半径和对应的回文中心，其中c为回文中心的位置，r为c向右能够扩展的最远距离。我们还需要一个变量i来遍历字符串，并维护当前能够快速推导出的回文半径p[i]的值。具体来说，我们先假设p[i]等于1，然后利用已知信息尽可能地扩大p[i]的大小，直到p[i]无法再增加为止。这里需要注意的是，我们需要将i映射到新字符串中的位置，即将原来的下标乘以2并加上1。

rust代码实现

fn good2(str: &str) -> i32 {
    if str.len() == 1 {
        return 0;
    }

    let p_arr = manacher(str);
    let s = str.as_bytes();
    let n = s.len();
    let mut range = 0;
    for (l, r) in (0..n).zip((0..n).rev()) {
        if l <= r && s[l] == s[r] {
            range += 1;
        } else {
            break;
        }
    }

    let mut ans = 0;
    for l in 0..n {
        for r in l..n {
            if l < n - r - 1 {
                if range >= l as i32 && check(&p_arr, r + 1, n - l - 1) {
                    ans += 1;
                }
            } else if l > n - r - 1 {
                if range >= n as i32 - r as i32 - 1 && check(&p_arr, n - r - 1, l - 1) {
                    ans += 1;
                }
            } else {
                if range >= l as i32 {
                    ans += 1;
                }
            }
        }
    }
    ans - 1
}

fn manacher(s: &str) -> Vec<i32> {
    let str = manacher_string(s);
    let mut p_arr = vec![0; str.len()];
    let mut c = -1;
    let mut r = -1;

    for i in 0..str.len() {
        p_arr[i] = if r > i as i32 {
            p_arr[(2 * c - i as i32) as usize].min(r - i as i32)
        } else {
            1
        };
        while i as i32 + p_arr[i] < str.len() as i32
            && (i as i32 - p_arr[i]) > -1
            && str[(i as i32 + p_arr[i]) as usize] == str[(i as i32 - p_arr[i]) as usize]
        {
            p_arr[i] += 1;
        }
        if i as i32 + p_arr[i] > r {
            r = i as i32 + p_arr[i];
            c = i as i32;
        }
    }
    p_arr
}

fn manacher_string(s: &str) -> Vec<u8> {
    let char_arr = s.as_bytes();
    let mut res = vec![0; s.len() * 2 + 1];
    let mut index = 0;
    for i in 0..res.len() {
        if i & 1 == 0 {
            res[i] = '#' as u8
        } else {
            res[i] = char_arr[index];
            index += 1;
        }
    }

    res
}

fn check(p_arr: &Vec<i32>, l: usize, r: usize) -> bool {
    let n = r - l + 1;
    let l = l * 2 + 1;
    let r = r * 2 + 1;
    p_arr[(l + r) / 2] - 1 >= n as i32
}

算法复杂度

时间复杂度：O(n)，其中n是字符串的长度。需要遍历整个字符串，并且每个位置只会被遍历一次。

空间复杂度：O(n)。需要使用额外的数组存储回文半径的信息，以及将字符串转换为新的格式。

完整代码

use rand::Rng;
use std::time::Instant;

fn good1(str: &str) -> i32 {
    let n = str.len();
    let mut ans = 0;
    for i in 0..n {
        for j in i..n {
            if is_palindrome(&(str[0..i].to_owned() + &str[j + 1..])) {
                ans += 1;
            }
        }
    }
    return ans - 1;
}

fn is_palindrome(str: &str) -> bool {
    let bytes = str.as_bytes();
    let mut l = 0;
    let mut r = bytes.len() as i32 - 1;

    while l <= r {
        if bytes[l as usize] != bytes[r as usize] {
            return false;
        }
        l += 1;
        r -= 1;
    }
    return true;
}

fn good2(str: &str) -> i32 {
    if str.len() == 1 {
        return 0;
    }

    let p_arr = manacher(str);
    let s = str.as_bytes();
    let n = s.len();
    let mut range = 0;
    for (l, r) in (0..n).zip((0..n).rev()) {
        if l <= r && s[l] == s[r] {
            range += 1;
        } else {
            break;
        }
    }

    let mut ans = 0;
    for l in 0..n {
        for r in l..n {
            if l < n - r - 1 {
                if range >= l as i32 && check(&p_arr, r + 1, n - l - 1) {
                    ans += 1;
                }
            } else if l > n - r - 1 {
                if range >= n as i32 - r as i32 - 1 && check(&p_arr, n - r - 1, l - 1) {
                    ans += 1;
                }
            } else {
                if range >= l as i32 {
                    ans += 1;
                }
            }
        }
    }
    ans - 1
}

fn manacher(s: &str) -> Vec<i32> {
    let str = manacher_string(s);
    let mut p_arr = vec![0; str.len()];
    let mut c = -1;
    let mut r = -1;

    for i in 0..str.len() {
        p_arr[i] = if r > i as i32 {
            p_arr[(2 * c - i as i32) as usize].min(r - i as i32)
        } else {
            1
        };
        while i as i32 + p_arr[i] < str.len() as i32
            && (i as i32 - p_arr[i]) > -1
            && str[(i as i32 + p_arr[i]) as usize] == str[(i as i32 - p_arr[i]) as usize]
        {
            p_arr[i] += 1;
        }
        if i as i32 + p_arr[i] > r {
            r = i as i32 + p_arr[i];
            c = i as i32;
        }
    }
    p_arr
}

fn manacher_string(s: &str) -> Vec<u8> {
    let char_arr = s.as_bytes();
    let mut res = vec![0; s.len() * 2 + 1];
    let mut index = 0;
    for i in 0..res.len() {
        if i & 1 == 0 {
            res[i] = '#' as u8
        } else {
            res[i] = char_arr[index];
            index += 1;
        }
    }

    res
}

fn check(p_arr: &Vec<i32>, l: usize, r: usize) -> bool {
    let n = r - l + 1;
    let l = l * 2 + 1;
    let r = r * 2 + 1;
    p_arr[(l + r) / 2] - 1 >= n as i32
}

// 为了测试
fn random_string(n: usize, v: usize) -> String {
    let mut str = vec![0 as u8; n];
    for i in 0..n {
        str[i] = (rand::thread_rng().gen_range(0, v) + 'a' as usize) as u8;
    }
    String::from_utf8(str).unwrap()
}

// 为了测试
fn main() {
    let n = 50;
    let v = 3;
    let test_time = 5000;
    println!("功能测试开始");
    for _ in 0..test_time {
        let n = rand::thread_rng().gen_range(1, n + 1);
        let str = random_string(n, v);
        let ans1 = good1(&str);
        let ans2 = good2(&str);
        if ans1 != ans2 {
            println!("出错了!");
            println!("{}", ans1);
            println!("{}", ans2);
            break;
        }
    }
    println!("功能测试结束");

    println!("性能测试开始");
    let n = 3000;
    let v = 26;
    let str = random_string(n, v);
    println!("字符串的长度 : {}", n);
    println!("小写字符种类 : {}", v);
    let start = Instant::now();
    let ans1 = good1(&str);
    let end = Instant::now();
    println!("方法1(暴力方法)答案 : {}", ans1);
    println!("方法1(暴力方法)运行时间 : {:?}", end - start);
    let start = Instant::now();
    let ans2 = good2(&str);
    let end = Instant::now();
    println!("方法2(正式方法)答案 : {}", ans2);
    println!("方法2(正式方法)运行时间 : {:?}", end - start);
    println!("性能测试结束");
}

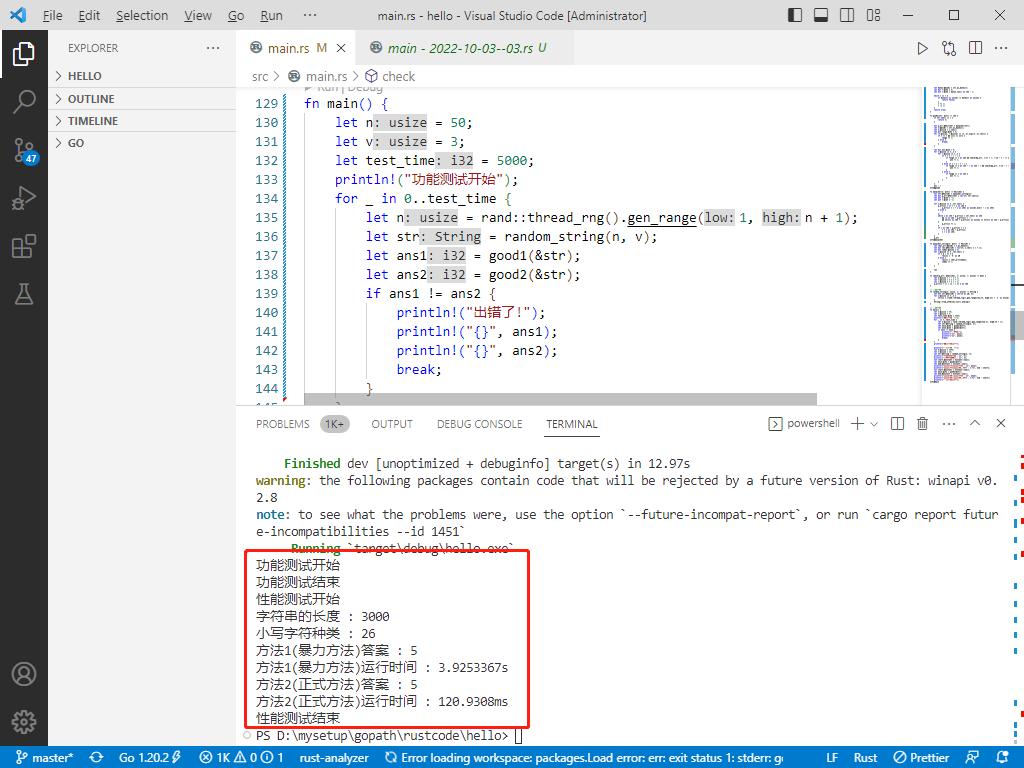
运行结果