LeetCode------递归（爬楼梯）

1、递归

• 1、一个问题的解可以分解为几个子问题的解。
• 2、这个问题与分解之后的子问题，除了数据规模不同，求解思路完全一样
• 3、存在基线/终止条件

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/climbing-stairs

题目
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

注意：给定 n 是一个正整数。

示例 1：

输入： 2
输出： 2
解释： 有两种方法可以爬到楼顶。
1.  1 阶 + 1 阶
2.  2 阶

示例 2：

输入： 3
输出： 3
解释： 有三种方法可以爬到楼顶。
1.  1 阶 + 1 阶 + 1 阶
2.  1 阶 + 2 阶
3.  2 阶 + 1 阶

推导递归公式：
F(1) =1
F(2) =2
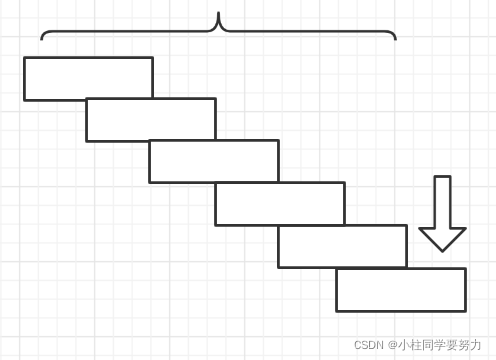
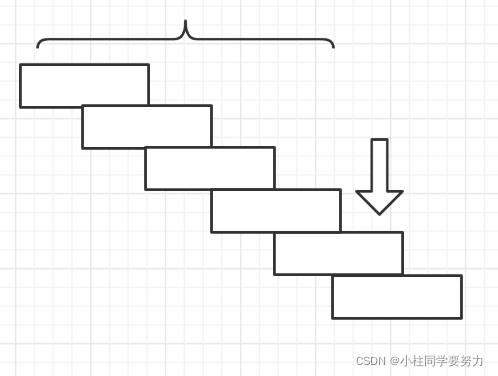
当n>=3时，第一次要么走一个台阶，然后剩余n-1个台阶要走。第一次走两个台阶，然后就要剩余n-2个台阶要走。
推导出递归公式

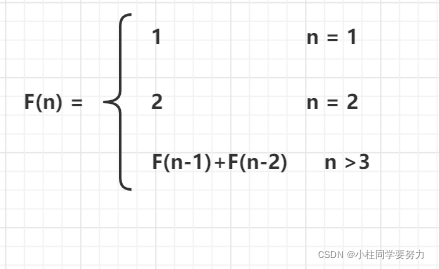
第一种代码实现

public int climbStairs(int n) {
        if(n == 1) return 1;
        if(n == 2) return 2;
      return climbStairs(n-1)+climbStairs(n-2);
      }

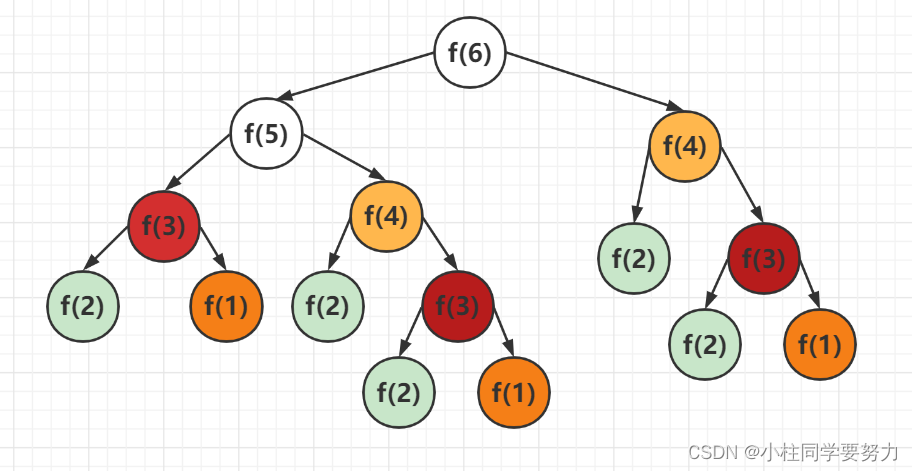
实现结果，时间超时
假如使用这种代码实现，从图中可以看出，每次都会重复计算已有的数据。怎样避免这种情况呢？可以将每次计算出来的结果存储起来，在计算之前先查询存储的数据是否存在。如果存在直接使用，不用再次计算。可以使用hashMap来存储计算的值<key,value>

代码改进

 private Map<Integer,Integer> storeMap = new HashMap<>();
    public int climbStairs(int n) {
        if(n == 1) return 1;
        if(n == 2) return 2;
        if(null != storeMap.get(n)){
            return storeMap.get(n);
        }else{
            int result = climbStairs(n-1)+climbStairs(n-2);
            storeMap.put(n,result);
            return result;
        }

    }

另外一种解法，从下往上的形式

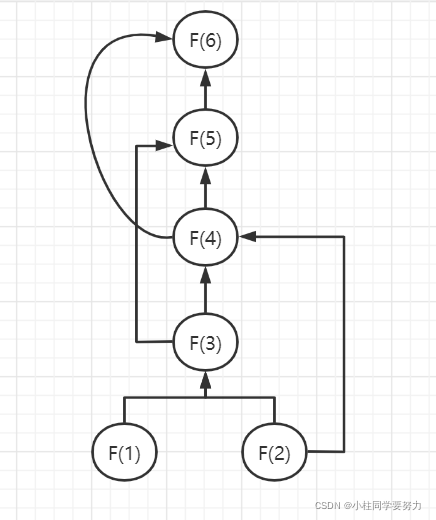
代码实现

 public int climbStairs(int n){
        if(n == 1) return 1;
        if(n == 2) return 2;
        int result = 0;
        int pre = 2;
        int prePre = 1;
        for(int i = 3;i<=n;i++){
            result = pre +prePre;
            prePre = pre;
            pre = result;
        }
        return result;
    }