[学习笔记]平衡树（Splay）——旋转的灵魂舞蹈家

1.简介

首先要知道什么是二叉查找树。

这是一棵二叉树，每个节点最多有一个左儿子，一个右儿子。

它能支持查找功能。

具体来说，每个儿子有一个权值，保证一个节点的左儿子权值小于这个节点，右儿子权值大于这个节点。

显然可以证明，这个树的中序遍历就是树上的序列从小到大排序后的结果。

我们插入一个值，就类似二分，从根往下找，直到进入一个空节点，然后插入。

查询的时候，比如查询前驱后继第k大等等，本质上都是通过比较左右儿子的权值/子树大小等来决策。

由于和节点的加入顺序有关，

所以，二叉查找树这样可以被轻松卡成一条链，然后每次查询链的底部，就卡成一次O(n)的了。

我们发现，同一个正确的中序遍历下的二叉查找树可能形态有很多。

而如果一个二叉查找树是满的二叉查找树，那么树高就是logn的，查询复杂度O(logn)非常可观。

所以，我们能不能通过一些手段，使得这棵二叉查找树总是能保持在logn的树高左右呢？

如果树高能够保证在logn的话，那么就称这个树是平衡的。

这也是平衡树的由来。

所以，平衡树一种能维持树高为logn的二叉查找树。

属于高级数据结构。

2.平衡树分类（查询均摊logn）

treap：

tree+heap

维护中序遍历之外，每个点随机一个优先级。

根据优先级，进行左旋或者右旋。

splay

直接双旋保证复杂度。

可以证明。（我不会，记住就好了）

fhq 非旋转treap

SBT ？？

RBT 红黑树，map的实现。

替罪羊树？？

3.treap及操作

单旋，把儿子和父亲交换。

分为左旋右旋。

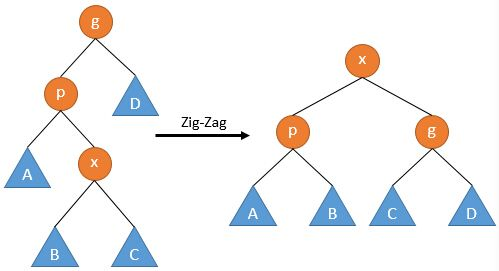
4.Splay及操作

没有优先值，但是采用双旋。

每次查询或者加入一个点，都把这个点旋转到根。

双旋的巧妙之处：

1.永远单旋是不够的。因为一条链转完还是一条链。

2.双旋一定程度上会把链缩短。

5.Splay的利用（每次最后都要splay到根）

单点操作：

①加入一个权值。从顶向下找，找到空节点加入。

②删除一个权值。找到这个权值节点，splay到根，把这个节点的后继splay到根的右儿子。

删除这个点。把根设为右儿子。（没有后继，那直接就是左儿子）

（也可以仿照区间删除的方法）

③单点加。同上。

区间操作：

通性：把l-1旋转到根。r+1旋转到根的右儿子。r+1左儿子的子树就是待处理区间。

可以支持懒标记。

懒标记和普通线段树的懒标记一样，作用点直接处理。然后打上标记。

标记必须支持合并、下放。

①区间加：提出区间后，r+1左儿子sum标记

②区间翻转：打翻转标记。同时交换左右儿子。

③区间删除：提出区间，后删除。

④区间插入：不能一个个insert，会被卡成n^2。

x到根，x+1到根右儿子。把要加入的数分治地建成一棵小平衡树。（分治直接保证logn树高）

然后接到x+1的左儿子。

查询操作：

一律先提出区间，然后直接查询根的右儿子的左儿子。

①区间求最大子段和：同线段树。每个节点代表一个区间，维护区间左起最大值，区间右起最大值，区间最大子段和，区间和。

提取完区间，直接查询。

②区间和。

如果出题人丧心病狂，让你维护一个序列，支持以上所有操作怎么办？

以及更多具体操作见：[NOI2005]维护数列——平衡树观止

upda:2018.11.14

Splay还有一个用途：LCT维护实链。

[学习笔记]动态树Link-Cut-Tree

6.数据结构的通性

1.数据结构的题目往往可以O(n^2)暴力写部分分。

考虑我们为什么要用数据结构，什么时候用。

数据结构：二叉堆，左偏树，tire树，栈，队列，哈希，链表，树状数组，并查集，分块，点分治，线段树，动态开点线段树，主席树，二叉查找树，平衡树

①维护正确性。hash主要针对的就是这一点。

②维护复杂度。包括空间和时间复杂度。

空间：主席树，动态开点线段树

时间：剩下的大部分。

还有一些：trie，队列，栈。

数据结构往往都是从维护这两部分的角度出发设计。

2.要分清数据结构和原序列、树本身，否则容易懵。

3.抓住数据结构（尤其平衡树）的形态，就比较容易理解，并且还能推理构造出其他的操作。