空洞卷积(dilated Convolution) 与感受野（Receptive Field）

一、空洞卷积

空洞卷积是是为了解决基于FCN思想的语义分割中，输出图像的size要求和输入图像的size一致而需要upsample，但由于FCN中使用pooling操作来增大感受野同时降低分辨率，导致upsample无法还原由于pooling导致的一些细节信息的损失的问题而提出的。为了减小这种损失，自然需要移除pooling层，因此空洞卷积应运而生。

所谓空洞卷积，有一种理解就是在卷积核中注入空洞（即0），注入的空洞的数量由参数dilation决定，以 卷积核为例，dilation=2即在卷积核每行每列中间加0 ，将卷积核变为 。如下图所示：

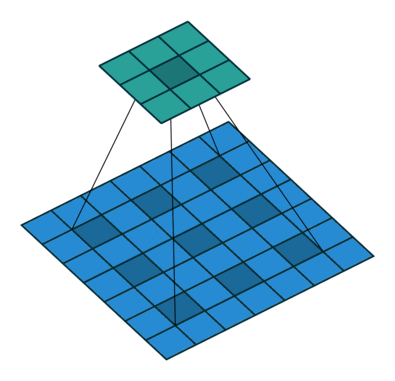
二、空洞卷积核的计算

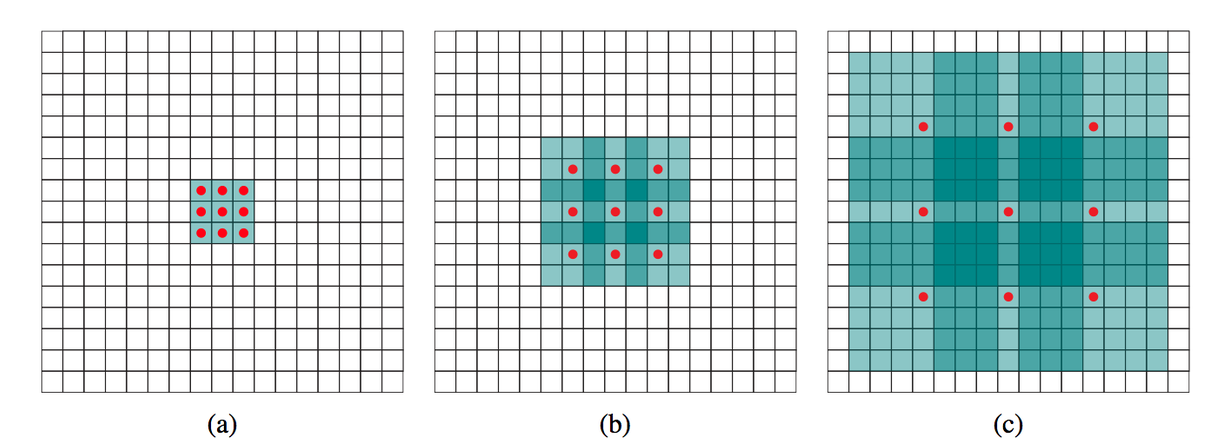
(a) 普通卷积，1-dilated convolution，卷积核的感受野为3x33×3
(b) 扩张卷积，2-dilated convolution，卷积核的感受野为7x77×7
(c) 扩张卷积，4-dilated convolution，卷积核的感受野为15x1515×15

由以上可归纳，当普通卷积核大小为ksize（如上图ksize=3）的时候，n-dilated convolution的膨胀卷积核大小为：

[(n-1)*(ksize+1)+ksize]×[(n-1)*(ksize+1)+ksize]

有了这个公式，当给定n和ksize，就可以计算出膨胀卷积核，然后在以下方法计算出感受野即可。

三、空洞卷积的感受野

　　OUT = (IN − FILTER + 2×PADDING )/STRIDE+1

• IN：输入Feature Map
• OUT：输出Feature Map
• FILTER：卷积核的尺寸
• PADDING：补零圈数
• STRIDE：滑动步长

卷积操作就是IN->OUT的过程，而求感受野是从OUT->IN的过程。假设不考虑PADDING，那么卷积公式变成：

　　OUT = (IN − FILTER )/STRIDE+1

因此，OUT->IN的，

　　IN = (OUT-1)×STRIDE+FILTER

计算某一层的一个特征图上的一个像素在原图上的感受野，就从该像素（OUT=1）开始，向前推算（使用FOR循环）。

这里的IN就是对应的感受野r。

OUT代表前一层的输出m。

FILTER：ksize

STRIDE：stride

##################################

以下内容来自

知乎：https://zhuanlan.zhihu.com/p/43784441

作者：机器学习学习之路

##################################

所以有cnn感受野计算公式： 这里 为本层感受野， 上层感受野， 卷积或池化的步长， 卷积核大小。例子如下（初始感受野大小为1）：

卷积(stride=1)： 感受野为

池化(stride=2)： 感受野为

卷积(stride=3)： 感受野为

空洞卷积的感受野计算方法和上面相同所谓的空洞可以理解为扩大了卷积核的大小，下面来介绍一下空洞卷积的感受野变化（卷积核大小为 ，stride=1，下面的卷积过程后面的以前面的为基础）：

1-dilated conv：rate=1的卷积其实就是普通 因此 （ ）卷积因此感受野为

2-dilated conv：rate=2可以理解为将卷积核变成了 ，因此 （ ）感受野大小为 。

4-dilated conv：rate=3可以理解为将卷积核变成了 因此 （ ）感受野大小为 15×15

可以看到将卷积以上面的过程叠加感受野变化会指数增长，感受野公式为 。

####################################