动态规划 70.climbing Stairs

1. 记忆化搜索 - 自上向下的解决问题：使用vector来保存每次计算的结果，如果下次再碰到同样的需要计算的式子就不需要重复计算了。

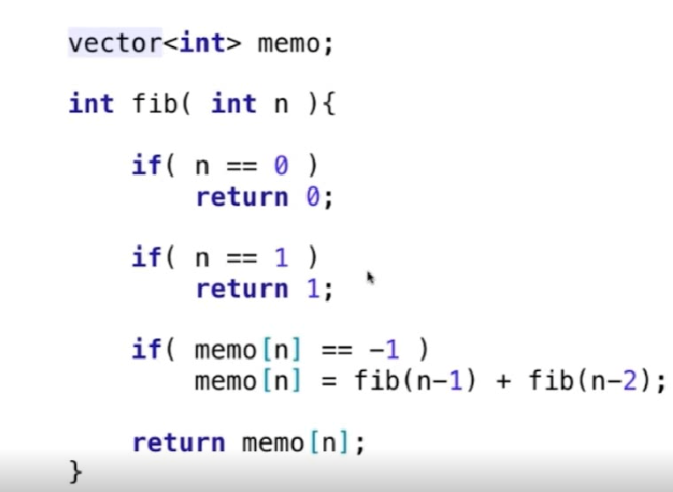
2. 动态规划 - 自下向上的解决问题

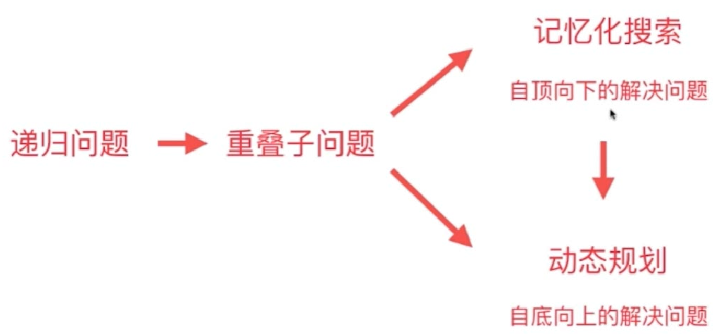
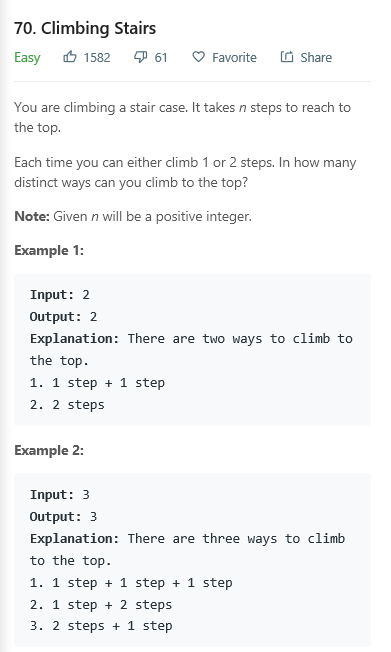
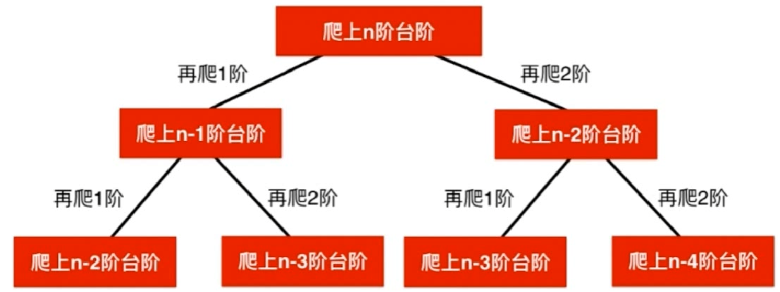
解法一：自顶向下

解法二：自底向上

class Solution {

private:
    vector<int> memo;

    int calcWays(int n){

        if(n==) return ;   //一个台阶都没有
        if(n==) return ;
        //if(n==2) return 2; //有两种解决方法：一次迈一步，迈两次；一次迈两步
        if(memo[n] == -)
            memo[n] = calcWays(n-) + calcWays(n-);
        //在第n-1阶台阶迈一步或者在第n-2阶台阶迈两步
        return memo[n];
    }

public:
    int climbStairs(int n) {
        //n为台阶数
        memo = vector<int>(n+,-);   //memo初始化为n+1个-1
        return calcWays(n);
    }
};

class Solution {

public:
    int climbStairs(int n) {
        //n为台阶数
        vector<int> memo(n+,-);   //memo初始化为n+1个-1
        memo[] = memo[] = ;
        for(int i=;i<=n;i++)
            memo[i] = memo[i-] + memo[i-];
        return memo[n];
    }
};

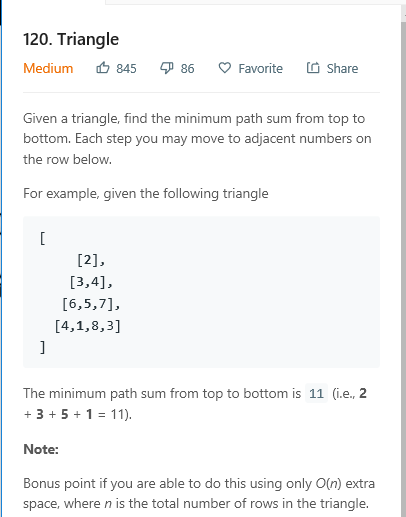
注意：从2只能移动到3和4；从3只能移动到6和5.

思路：设从位置（i,j）达到底部的最小路径和为MP(i,j)；根据约束条件，从位置（i,j）只能达到下一行的（i+1,j）和（i+1,j+1）两个位置；

前面的思路是自顶向下的，如果采用自底向上的求解思路，最后的sum[0]是要的结果。可以申请一个一维数组初始化为三角形数阵底部向量，逐步向上计算更新，空间复杂度为O(n)

class Solution {
public:
    int minimumTotal(vector<vector<int>>& triangle) {
        int length = triangle.size();
        if(length==) return ;
        if(length==) return triangle[][];
        vector<int> sum = triangle[length-];   //初始化sum为三角形底部的向量

        for(int i=length-;i>=;i--){
            for(int j=;j<triangle[i].size();j++)
                sum[j] = min(triangle[i][j]+sum[j], triangle[i][j]+sum[j+]);
        }

        return sum[];
    }
};

这个解法是重做了一遍题想到的，感觉比上一个解法有点麻烦，还容易索引溢出。

class Solution {
public:
    int minimumTotal(vector<vector<int>>& triangle) {
        if(triangle.empty()) return ;
        int row = triangle.size();
        int column = triangle[row-].size();
        int dp[row][column+];
        for(int i=; i<row; i++){
            for(int j=; j<column+; j++){
                dp[i][j] = INT_MAX;
            }
        }
        dp[][] = triangle[][];

        for(int i = ; i < row; i++){
            for(int j=; j<=i+; j++){

                dp[i][j] = min(dp[i-][j-], dp[i-][j]) + triangle[i][j-];
            }
        }

        sort(dp[row-], dp[row-]+column+);
        return dp[row-][];
    }
};

题目：给定一个包含非负整数的 m x n 网格，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：每次只能向下或者向右移动一步。

示例:

输入:
[[1,3,1],
[1,5,1],
[4,2,1]]
输出: 7
解释: 因为路径 1→3→1→1→1 的总和最小。

思路

以输入为 3*3 的网格为例，其中 m=3，n=3
[1,3,1]
[1,5,1]
[4,2,1]
由于每次只能向下或者向右移动，则每一步结果为当前值＋min(上边一步，左边一步)，即 dp[i][j] = grid[i][j] + min(dp[i-1][j], dp[i][j-1])

注意：不要忘记dp[0][0]的初始化。

class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) {
        if(grid.size() == ) return ;
        int m = grid.size();
        int n = grid[].size();
        int dp[m][n];   //m行n列的一个二维数组
        dp[][] = grid[][];
        //初始化边界
        for(int i = ; i<m; i++){
            dp[i][] = grid[i][] + dp[i-][];   //最左边一列的值只能是当前格子+上面一个
        }
        for(int i=;i<n;i++){
            dp[][i] = grid[][i] + dp[][i-];   //最上面一行的值只能是当前格子+左边一个
        }
        for(int i=;i<m;i++){
            for(int j=;j<n;j++)
                dp[i][j] = grid[i][j] + min(dp[i-][j], dp[i][j-]);
        }

        return dp[m-][n-];
    }
};

解法二：又做了一遍，自己想出来了思路

1）设置一维数组 dp[i] 为 当前行存储的到该索引的最小和；

2）初始化dp为grid的第一行，即  dp[0] = grid[0][0]; 然后接下来dp[i] = dp[i-1] + grid[0][i];

3) 状态方程：dp[j] = min(dp[j-1]+grid[i][j], dp[j]+grid[i][j]); //取左边或上面到该索引的最小值

4）dp最左边一列只能从上面走到。

class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) {
        int n = grid.size();
        int m = grid[].size();
        int dp[m] = {};
        dp[] = grid[][];
        for(int i=; i<m;i++){
            dp[i] = dp[i-] + grid[][i];

        }

        for(int i=; i<n; i++){
            for(int j=; j<m ; j++){
                if(j==)
                    dp[j] = dp[j] + grid[i][j];
                else{
                    dp[j] = min(dp[j-]+grid[i][j], dp[j]+grid[i][j]);
                }
            }
        }
        return dp[m-];
    }
};