洛谷 P2387 [NOI2014]魔法森林 解题报告

P2387 [NOI2014]魔法森林

题目描述

为了得到书法大家的真传，小 E 同学下定决心去拜访住在魔法森林中的隐 士。魔法森林可以被看成一个包含 n 个节点 m 条边的无向图，节点标号为 1,2,3,…,n，边标号为 1,2,3,…,m。初始时小 E 同学在 1 号节点，隐士则住在 n 号节点。小 E 需要通过这一片魔法森林，才能够拜访到隐士。

魔法森林中居住了一些妖怪。每当有人经过一条边的时候，这条边上的妖怪 就会对其发起攻击。幸运的是，在 1 号节点住着两种守护精灵：A 型守护精灵与 B 型守护精灵。小 E 可以借助它们的力量，达到自己的目的。

只要小 E 带上足够多的守护精灵，妖怪们就不会发起攻击了。具体来说，无 向图中的每一条边 ei 包含两个权值 ai 与 bi 。若身上携带的 A 型守护精灵个数不 少于 ai ，且 B 型守护精灵个数不少于 bi ，这条边上的妖怪就不会对通过这条边 的人发起攻击。当且仅当通过这片魔法森林的过程中没有任意一条边的妖怪向 小 E 发起攻击，他才能成功找到隐士。

由于携带守护精灵是一件非常麻烦的事，小 E 想要知道，要能够成功拜访到 隐士，最少需要携带守护精灵的总个数。守护精灵的总个数为 A 型守护精灵的 个数与 B 型守护精灵的个数之和。

输入输出格式

输入格式：

输入文件的第 1 行包含两个整数 n,m，表示无向图共有 n 个节点，m 条边。 接下来 m 行，第i+ 1 行包含 4 个正整数 Xi,Yi,ai,bi，描述第i条无向边。 其中Xi与 Yi为该边两个端点的标号，ai 与 bi 的含义如题所述。 注意数据中可能包含重边与自环。

输出格式：

输出一行一个整数：如果小 E 可以成功拜访到隐士，输出小 E 最少需要携 带的守护精灵的总个数；如果无论如何小 E 都无法拜访到隐士，输出“-1”（不 含引号）。

说明

---

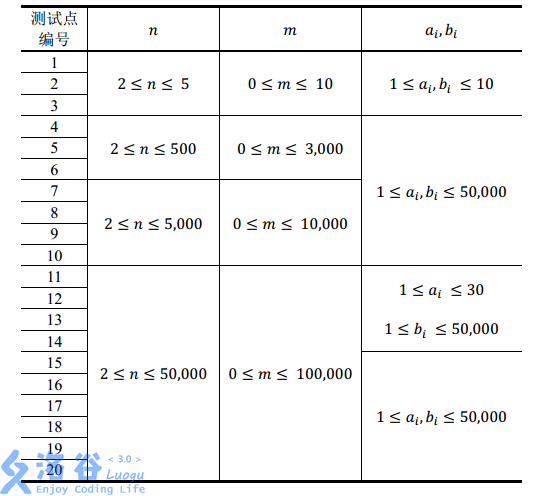
各种奇奇怪怪的二分确定是错误的

我用神奇的二分+spfa错解混了50分

LCT 正解思路：

排序一维，按顺序加边，当加出环的时候，去掉最大的一条边。

若1与n联通，则更新答案

因为lct处理的是点权，所以我们队每条边都建一个点

---

Code:

#include <cstdio>
#include <algorithm>
#define ls ch[now][0]
#define rs ch[now][1]
#define fa par[now]
const int N=150010;
const int inf=0x7fffffff;
int min(int x,int y){return x<y?x:y;}
int ch[N][2],par[N],dat[N],ms[N],tag[N],loc[N],s[N],tot;
int ans=inf,n,m;
bool isroot(int now){return ch[fa][0]==now||ch[fa][1]==now;}
int identity(int now){return ch[fa][1]==now;}
void connect(int f,int now,int typ){fa=f;ch[f][typ]=now;}
void Reverse(int now){int tmp=ls;ls=rs,rs=tmp;tag[now]^=1;}
void updata(int now)
{
    if(ms[ls]>ms[rs]) ms[now]=ms[ls],loc[now]=loc[ls];
    else ms[now]=ms[rs],loc[now]=loc[rs];
    if(dat[now]>ms[now]) ms[now]=dat[now],loc[now]=now;
}
void Rotate(int now)
{
    int p=fa,typ=identity(now);
    connect(p,ch[now][typ^1],typ);
    if(isroot(p)) connect(par[p],now,identity(p));
    else fa=par[p];
    connect(now,p,typ^1);
    updata(p),updata(now);
}
void push_down(int now)
{
    if(tag[now])
    {
        if(ls) Reverse(ls);
        if(rs) Reverse(rs);
        tag[now]^=1;
    }
}
void splay(int now)
{
    while(isroot(now)) s[++tot]=now,now=fa;
    s[++tot]=now;
    while(tot) push_down(s[tot--]);
    now=s[1];
    for(;isroot(now);Rotate(now))
        if(isroot(fa))
            Rotate(identity(now)^identity(fa)?now:fa);
}
void access(int now)
{
    for(int las=0;now;las=now,now=fa)
        splay(now),rs=las,updata(now);
}
void evert(int now)
{
    access(now);
    splay(now);
    Reverse(now);
}
void link(int u,int v)
{
    evert(u);
    par[u]=v;
}
void cat(int u,int v)
{
    evert(u);
    access(v);
    splay(v);
    ch[v][0]=par[u]=0;
    updata(v);
}
int findroot(int now)
{
    access(now);
    splay(now);
    while(ls) now=ls;
    return now;
}
void query(int u,int v,int &mx,int &pos)
{
    evert(u);
    access(v);
    splay(v);
    pos=loc[v],mx=ms[v];
}
struct node
{
    int u,v,a,b;
    friend bool operator <(node n1,node n2)
    {
        return n1.a<n2.a;
    }
}e[N];
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=m;i++)
        scanf("%d%d%d%d",&e[i].u,&e[i].v,&e[i].a,&e[i].b);
    std::sort(e+1,e+1+m);
    for(int i=1;i<=m;i++)
        dat[i+n]=ms[i+n]=e[i].b,loc[i+n]=i+n;
    for(int i=1;i<=m;i++)
    {
        int u=e[i].u,v=e[i].v,mx,pos;
        if(u==v) continue;
        if(findroot(u)==findroot(v))
        {
            query(u,v,mx,pos);
            if(mx>e[i].b)
            {
                cat(pos,e[pos-n].u),cat(pos,e[pos-n].v);
                link(n+i,u),link(n+i,v);
            }
        }
        else
            link(n+i,u),link(n+i,v);
        if(findroot(1)==findroot(n))
        {
            query(1,n,mx,pos);
            ans=min(ans,mx+e[i].a);
        }
    }
    if(ans==inf) printf("-1\n");
    else printf("%d\n",ans);
    return 0;
}

---

2018.8.22