Hack Programming

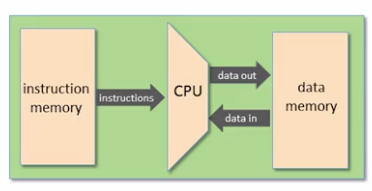
计算机由ROM（instruction memory）、RAM（data memory）、CPU组成，其关系如下图

在计算中存在3种寄存器：D、A、M。其中D是data register，A是address register，M是data/address register。

为对数据进行操作，存在两种指令：A-introduction，C-introduction，这也就是Hack Promramming的全部语法了。Hack Programming 属于一种 汇编语言（Assembly language），计算机处理的都是0/1，但不便于阅读编程，但汇编语言通过编译可以成为二进制语句。

A-introduction的语法就是 @ num，num可以是非负整数，也可以variable/LABEL，这个语句可以应用于三种情况：

1）赋值A。A是地址，比如@2，就是令当前的A=2，并可以对M = RAM[A]进行操作

2）指定寄存器RAM[A]。

3）指定下一条指令。这里的指定下一条指令一般是用于 @LABEL，实现goto功能，这一语句经过编译会变为 @ num，num是定义LABEL的下一行的行数。举例如下

注：关于variable：和LABEL不同，不需要在程序中申明，编译时会自动寻找可行的寄存器，比如@i，编译时会变为 @num，num表示寄存器的地址。

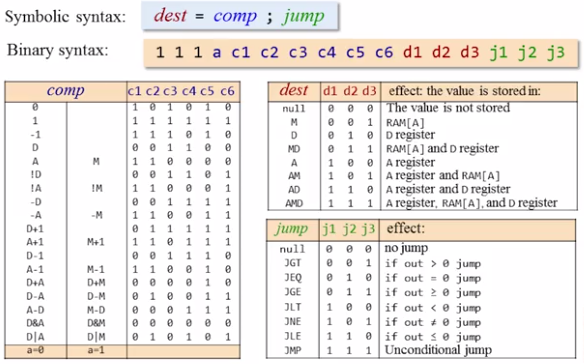
C-Instruction的语法如下，主要功能是实现运算和赋值。

此外，还有一个POINTER的概念，其实就是地址，在HACK编程的C指令中，只能用上面涉及到的语法，所以要实现赋值操作一般都是下面这样

// i = 100
@
D = A
@i
M = D

//修改SCREEN MAP第2个寄存器的值全为1
@SCREEN
D = A
A = A+
M = -

最后还有屏幕输出和键盘输入。

假设屏幕大小是256*512，计算机是16bit，那32个寄存器对应屏幕的一行，依次下推，这样用于屏幕输出的寄存器就需要256*512/16个；屏幕的每一个pixel都只有0/1，1的话就是黑色，要改变屏幕输出，其实通过要改变的像素点，找到相应寄存器的相应bit，再改变bit的值为1。

键盘输入只需要一个寄存器，一般会有个固定地址，当进行键盘输入时，其寄存器的值M就不为0，而是输入字符的对应码。

举个栗子：实现当进行键盘输入时，屏幕的头16个像素变黑，松开时变白

    @
    D = A
    @n
    M = D

    @SCREEN
    D = A
    @pointer
    M = D

    @isfill
    M = 

(LOOP)
    @KBD
    D = M;
    @FILL
    D;JNE

    @UNFILL
    D;JEQ

(FILL)
    @isfill
    D = M
    @LOOP
    D;JNE

    @pointer
    A = M
    M = -

    @isfill
    M = 

    @LOOP
    ;JMP

(UNFILL)
    @isfill
    D = M
    @LOOP
    D;JEQ

    @pointer
    A = M
    M = 

    @isfill
    M = 

    @LOOP
    ;JMP