LeetCode编程训练 - 合并查找(Union Find)

Union Find算法基础

Union Find算法用于处理集合的合并和查询问题，其定义了两个用于并查集的操作：

• Find: 确定元素属于哪一个子集，或判断两个元素是否属于同一子集
• Union: 将两个子集合并为一个子集

并查集是一种树形的数据结构，其可用数组或unordered_map表示：

Find操作即查找元素的root，当两元素root相同时判定他们属于同一个子集；Union操作即通过修改元素的root(或修改parent)合并子集，下面两个图展示了id[6]由6修改为9的变化：

  

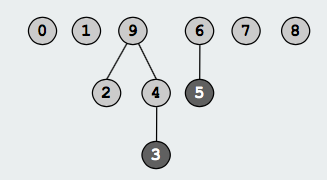
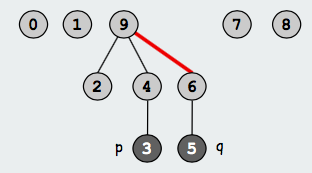
图片来源 这里

Union Find算法应用

Union Find可用于解决集合相关问题，如判断某元素是否属于集合、两个元素是否属同一集合、求解集合个数等，算法框架如下：

    //261. Graph Valid Tree
    bool validTree(int n, vector<pair<int, int>>& edges) {
        vector<int> num(n,-);
        for(auto edge:edges){
            //find查看两点是否已在同一集合
            int x=find(num,edge.first);
            int y=find(num,edge.second);
            if(x==y) return false;  //两点已在同一集合情况下则出现环
            //union让两点加入同一集合
            num[x]=y;
        }
        return n-==edges.size();
    }
    int find(vector<int>&num,int i){
        if(num[i]==-) return i;
        return find(num,num[i]);  //id[id[...id[i]...]]
    }

一些情况下为清晰和解偶会将Uinon Find实现为一个类，独立出明显的Union和Find两个操作。

相关LeetCode题：

261. Graph Valid Tree  题解

684. Redundant Connection  题解

547. Friend Circles  题解

947. Most Stones Removed with Same Row or Column  题解

200. Number of Islands  题解

 

算法优化

有两种常用的方法用来降低并查集树形结构的高度、以减少Uinon Find算法的时间复杂度，这两种方法是：

Weighting(或称作Ranking): 使用多一个数组记录每个集合的size，Uinon时将size小的集合挂到size大的集合下，例如：

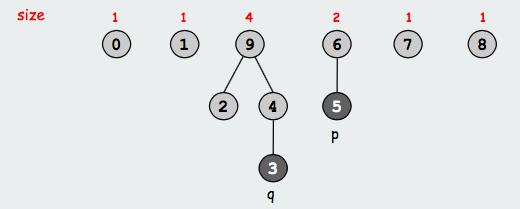
对3、5 Uinon，因3所在集合元素size 4大于5所在集合元素size 2，将6挂到9下而不是将9挂到6下。

Path compression: 对一个集合下的元素直接挂到root之下，而不是挂到其parent，path compression实现很简单只需在Find中加一行代码：

    string find(unordered_map<string,string>& root,string s){
        if(root[s]!=s)
            root[s]=find(root,root[s]);
        return root[s];
    }

加入path compression也能实现减少并查集树高度的效果，图示如下：

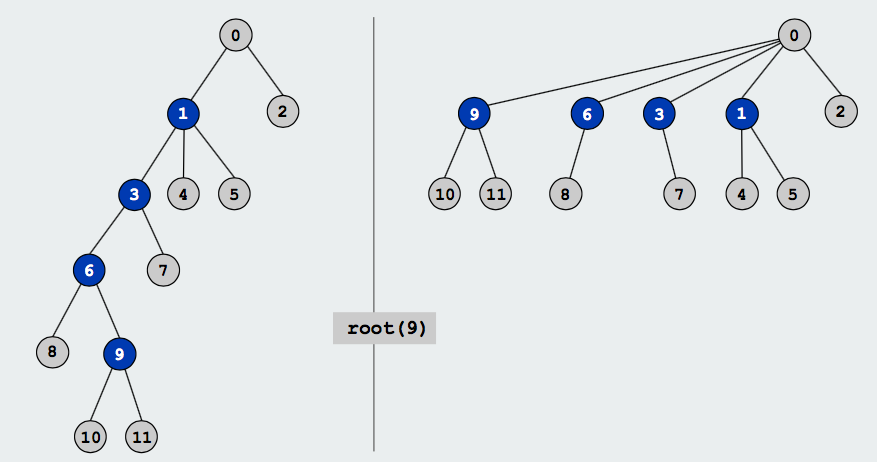
Weighting和Path compression两种方法可以同时使用，这样使得对N个元素进行M次Union Find操作的时间复杂度可以减少到 (M+N)lgN。因lgN随N的增长变化很小，所以整体算法时间复杂度接近于线性的时间复杂度。

相关LeetCode题：

128. Longest Consecutive Sequence  题解

924. Minimize Malware Spread  题解