支持向量机SVM（二）

【转载请注明出处】http://www.cnblogs.com/jerrylead

6 拉格朗日对偶（Lagrange duality）

先抛开上面的二次规划问题，先来看看存在等式约束的极值问题求法，比如下面的最优化问题：

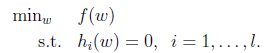
目标函数是f(w)，下面是等式约束。通常解法是引入拉格朗日算子，这里使用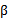来表示算子，得到拉格朗日公式为

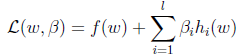
L是等式约束的个数。

然后分别对w和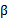求偏导，使得偏导数等于0，然后解出w和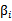。至于为什么引入拉格朗日算子可以求出极值，原因是f(w)的dw变化方向受其他不等式的约束，dw的变化方向与f(w)的梯度垂直时才能获得极值，而且在极值处，f(w)的梯度与其他等式梯度的线性组合平行，因此他们之间存在线性关系。（参考《最优化与KKT条件》）

然后我们探讨有不等式约束的极值问题求法，问题如下：

我们定义一般化的拉格朗日公式

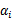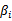这里的和都是拉格朗日算子。如果按这个公式求解，会出现问题，因为我们求解的是最小值，而这里的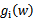已经不是0了，我们可以将调整成很大的正值，来使最后的函数结果是负无穷。因此我们需要排除这种情况，我们定义下面的函数：

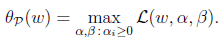
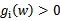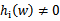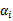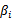这里的P代表primal。假设或者，那么我们总是可以调整和来使得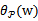有最大值为正无穷。而只有g和h满足约束时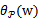，为f(w)。这个函数的精妙之处在于，而且求极大值。

因此我们可以写作

这样我们原来要求的min f(w)可以转换成求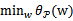了。

我们使用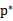来表示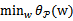。如果直接求解，首先面对的是两个参数，而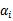也是不等式约束，然后再在w上求最小值。这个过程不容易做，那么怎么办呢？

我们先考虑另外一个问题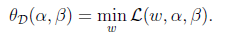

D的意思是对偶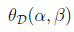，将问题转化为先求拉格朗日关于w的最小值，将和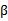看作是固定值。之后在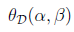求最大值的话：

这个问题是原问题的对偶问题，相对于原问题只是更换了min和max的顺序，而一般更换顺序的结果是Max Min(X) <= MinMax(X)。然而在这里两者相等。用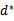来表示对偶问题如下：

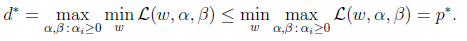
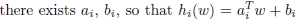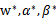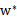下面解释在什么条件下两者会等价。假设f和g都是凸函数，h是仿射的（affine，）。并且存在w使得对于所有的i，。在这种假设下，一定存在使得是原问题的解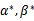，是对偶问题的解。还有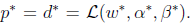另外，满足库恩-塔克条件（Karush-Kuhn-Tucker, KKT condition），该条件如下：

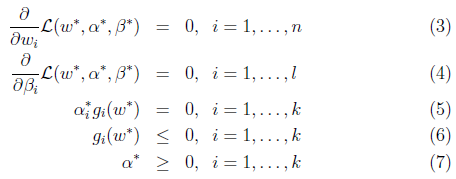
所以如果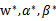满足了库恩-塔克条件，那么他们就是原问题和对偶问题的解。让我们再次审视公式（5），这个条件称作是KKT dual complementarity条件。这个条件隐含了如果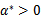，那么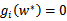。也就是说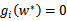，时，w处于可行域的边界上，这时才是起作用的约束。而其他位于可行域内部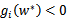（的）点都是不起作用的约束，其。这个KKT双重补足条件会用来解释支持向量和SMO的收敛测试。

这部分内容思路比较凌乱，还需要先研究下《非线性规划》中的约束极值问题，再回头看看。KKT的总体思想是将极值会在可行域边界上取得，也就是不等式为0或等式约束里取得，而最优下降方向一般是这些等式的线性组合，其中每个元素要么是不等式为0的约束，要么是等式约束。对于在可行域边界内的点，对最优解不起作用，因此前面的系数为0。

7 最优间隔分类器（optimal margin classifier）

重新回到SVM的优化问题：

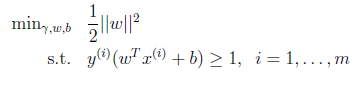
我们将约束条件改写为：

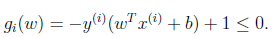
从KKT条件得知只有函数间隔是1（离超平面最近的点）的线性约束式前面的系数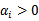，也就是说这些约束式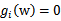，对于其他的不在线上的点(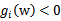)，极值不会在他们所在的范围内取得，因此前面的系数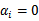.注意每一个约束式实际就是一个训练样本。

看下面的图：

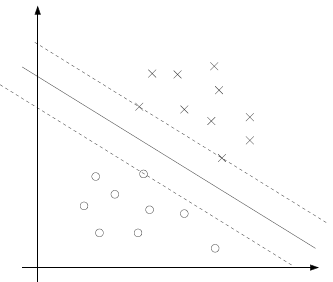
实线是最大间隔超平面，假设×号的是正例，圆圈的是负例。在虚线上的点就是函数间隔是1的点，那么他们前面的系数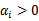，其他点都是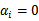。这三个点称作支持向量。构造拉格朗日函数如下：

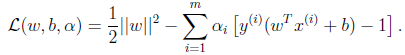
注意到这里只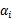有没有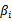是因为原问题中没有等式约束，只有不等式约束。

下面我们按照对偶问题的求解步骤来一步步进行，

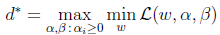
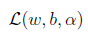首先求解的最小值，对于固定的，的最小值只与w和b有关。对w和b分别求偏导数。

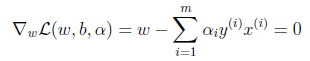
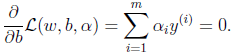
并得到

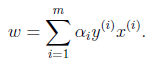
将上式带回到拉格朗日函数中得到，此时得到的是该函数的最小值（目标函数是凸函数）

代入后，化简过程如下：

　　最后得到

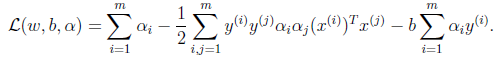
由于最后一项是0，因此简化为

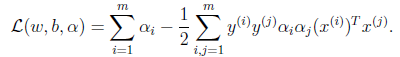
这里我们将向量内积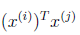表示为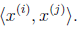

此时的拉格朗日函数只包含了变量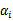。然而我们求出了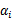才能得到w和b。

接着是极大化的过程，

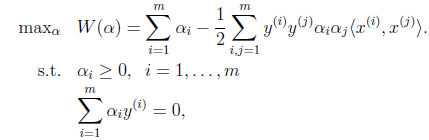
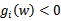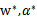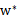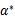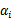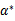前面提到过对偶问题和原问题满足的几个条件，首先由于目标函数和线性约束都是凸函数，而且这里不存在等式约束h。存在w使得对于所有的i，。因此，一定存在使得是原问题的解，是对偶问题的解。在这里，求就是求了。

如果求出了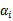，根据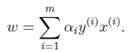即可求出w（也是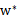，原问题的解）。然后

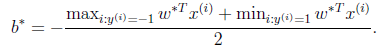
即可求出b。即离超平面最近的正的函数间隔要等于离超平面最近的负的函数间隔。

关于上面的对偶问题如何求解，将留给下一篇中的SMO算法来阐明。

这里考虑另外一个问题，由于前面求解中得到

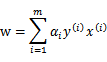
我们通篇考虑问题的出发点是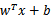，根据求解得到的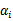，我们代入前式得到

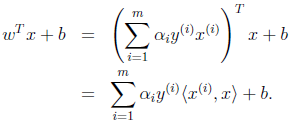
也就是说，以前新来的要分类的样本首先根据w和b做一次线性运算，然后看求的结果是大于0还是小于0,来判断正例还是负例。现在有了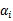，我们不需要求出w，只需将新来的样本和训练数据中的所有样本做内积和即可。那有人会说，与前面所有的样本都做运算是不是太耗时了？其实不然，我们从KKT条件中得到，只有支持向量的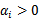，其他情况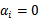。因此，我们只需求新来的样本和支持向量的内积，然后运算即可。这种写法为下面要提到的核函数（kernel）做了很好的铺垫。这是上篇，先写这么多了。