CRC算法及C实现

一、CRC算法原理  
　　CRC校验的基本思想是利用线性编码理论，在发送端根据要传送的k位二进制码序列，以一定的规则产生一个校 验用的监督码（既CRC码）r位，并附在信息后边，构成一个新的二进制码序列数共(k+r)位，最后发送出去。在接收端，则根据信息码和CRC码之间所遵循的规则进行检验，以确定传送中是否出错。
　　16位的CRC码产生的规则是先将要发送的二进制序列数左移16位（既乘以 ）后，再除以一个多项式，最后所得到的余数既是CRC码。

　　假设数据传输过程中需要发送15位的二进制信息 g=101001110100001，这串二进制码可表示为代数多项式g(x) = x^14 + x^12 + x^9 + x^8 + x^7 + x^5 + 1，其中g中第k位的值，对应g(x)中x^k的系数。将g(x)乘以x^m，既将g后加m个0，然后除以m阶多项式h(x)，得到的(m-1)阶余项 r(x)对应的二进制码r就是CRC编码。

h(x)可以自由选择或者使用国际通行标准，一般按照h(x)的阶数m，将CRC算法称为CRC-m，比如CRC-32、CRC-64等。国际通行标准可以参看http://en.wikipedia.org/wiki/Cyclic_redundancy_check

g(x)和h(x)的除运算，可以通过g和h做xor（异或）运算。比如将11001与10101做xor运算：

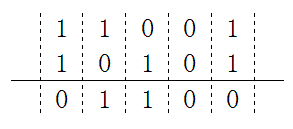
　　明白了xor运算法则后，举一个例子使用CRC-8算法求101001110100001的效验码。CRC-8标准的h(x) = x^8 + x^7 + x^6 + x^4 + x^2 + 1，既h是9位的二进制串111010101。

　　经过迭代运算后，最终得到的r是10001100，这就是CRC效验码。

　　通过示例，可以发现一些规律，依据这些规律调整算法：

1. 每次迭代，根据gk的首位决定b，b是与gk进行运算的二进制码。若gk的首位是1，则b=h；若gk的首位是0，则b=0，或者跳过此次迭代，上面的例子中就是碰到0后直接跳到后面的非零位。

 

2. 每次迭代，gk的首位将会被移出，所以只需考虑第2位后计算即可。这样就可以舍弃h的首位，将b取h的后m位。比如CRC-8的h是111010101，b只需是11010101。

※蓝色表示寄存器S的首位，是需要移出的，b根据S的首位选择0或者h。黄色是需要移入寄存器的位。S'是经过位移后的S。

查表法

同样是上面的那个例子，将数据按每4位组成1个block，这样g就被分成6个block。

下面的表展示了4次迭代计算步骤，灰色背景的位是保存在寄存器中的

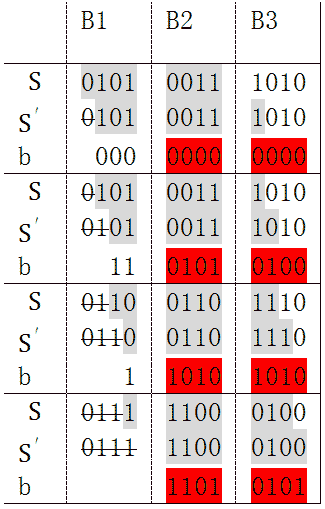
经4次迭代，B1被移出寄存器。被移出的部分，不我们关心的，我们关心的是这4次迭代对B2和B3产生了什么影响。注意表中红色的部分，先作如下定义：

B23 = 00111010
   b1 = 00000000
   b2 = 01010100
   b3 = 10101010
   b4 = 11010101
   b' = b1 xor b2 xor b3 xor b4

4次迭代对B2和B3来说,实际上就是让它们与b1,b2,b3,b4做了xor计算，既：

B23 xor b1 xor b2 xor b3 xor b4

可以证明xor运算满足交换律和结合律，于是：

B23 xor b1 xor b2 xor b3 xor b4 = B23 xor (b1 xor b2 xor b3 xor b4) = B23 xor b'

b1是由B1的第1位决定的，b2是由B1迭代1次后的第2位决定（既是由B1的第1和第2位决定），同理,b3和b4都是由B1决定。通过B1就可以计算出b'。另外，B1由4位组成，其一共2^4有种可能值。于是我们就可以想到一种更快捷的算法，事先将b'所有可能的值，16个值可以看成一个表；这样就可以不必进行那4次迭代，而是用B1查表得到b'值，将B1移出，B3移入，与b'计算，然后是下一次迭代。

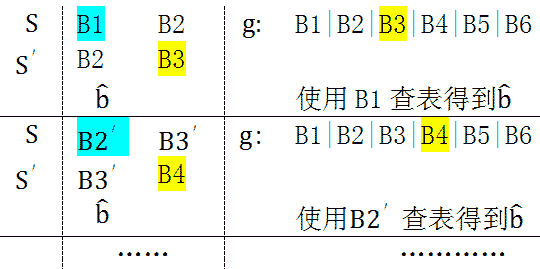
可看到每次迭代，寄存器中的数据以4位为单位移入和移出，关键是通过寄存器前4位查表获得，这样的算法可以大大提高运算速度。

上面的方法是半字节查表法，另外还有单字节和双字节查表法，原理都是一样的——事先计算出2^8或2^16个b'的可能值，迭代中使用寄存器前8位或16位查表获得b'。

反向算法

之前讨论的算法可以称为正向CRC算法，意思是将g左边的位看作是高位，右边的位看作低位。G的右边加m个0，然后迭代计算是从高位开始，逐步将低位加入到寄存器中。在实际的数据传送过程中，是一边接收数据，一边计算CRC码，正向算法将新接收的数据看作低位。

逆向算法顾名思义就是将左边的数据看作低位，右边的数据看作高位。这样的话需要在g的左边加m个0，h也要逆向，例如正向CRC-16算法h=0x4c11db8，逆向CRC-16算法h=0xedb88320。b的选择0还是h，由寄存器中右边第1位决定，而不是左边第1位。寄存器仍旧是向左位移，就是说迭代变成从低位到高位。

二、C语言实现

1、crc-8

crc8 c语言源程序

uint8 xCal_crc(uint8 *ptr,uint32 len)
{uint8 crc;
 uint8 i;
    crc = ;
    while(len--)
    {
       crc ^= *ptr++;
       ;i < ;i++)
       {
           if(crc & 0x01)
           {
               crc = (crc >> ) ^ 0x8C;
           };
       }
    }
    return crc;
}