P2258子矩阵

传送

一道看起来就很暴力的题。

这道题不仅暴力，还要用正确的姿势打开暴力。

因为子矩阵的参数有两个，一个行一个列（废话）

我们一次枚举两个参数很容易乱对不对？所以我们先枚举行，再枚举列

枚举完行，列，就计算一次当前子矩阵的分数，与ans取min。

代码：

但是复杂度会高到爆炸。来我们深吸一口O₂。

// luogu-judger-enable-o2
#include<bits/stdc++.h>
using namespace std;
int ma[][],n,m,r,c,ans=,ch[],cl[];
void js()
{  int an=;
    for(int i=;i<=r;i++)//求子矩阵左右的差的绝对值
        for(int j=;j<=c;j++)
         an+=abs(ma[ch[i]][cl[j]]-ma[ch[i]][cl[j-]]);
    for(int i=;i<=r;i++)//求上下的差的绝对值
        for(int j=;j<=c;j++)
         an+=abs(ma[ch[i]][cl[j]]-ma[ch[i-]][cl[j]]);
    ans=min(ans,an);
}
void dfs(int x,int y,int nr,int nc)//x:当前枚举的行在原矩阵中是第x行，y:当前枚举的列在原矩阵中是第y列，nr:将要枚举的行的数量，nc:将要枚举的列的数量
{
    if(nc==c+)
    {
        js();
        return;
    }
    if((x>n&&nr!=r+)||(y>m&&nc!=c+))return ;
    if(nr==r+)//当枚举完行了之后，枚举列
    {
        for(int i=y;i<=m;i++)
        {
            cl[nc]=i;
            dfs(x,i+,nr,nc+);
        }
    }
    else//枚举行
    {
        for(int i=x;i<=n;i++)
        {
            ch[nr]=i;
            dfs(i+,y,nr+,nc);
        }
    }
}
int main()
{
    scanf("%d%d%d%d",&n,&m,&r,&c);
    for(int i=;i<=n;i++)
     for(int j=;j<=m;j++)
      scanf("%d",&ma[i][j]);
    dfs(,,,);
    printf("%d",ans);
}

TTTLE

还是T成这种美丽的图形

你看它T的多有美感

好了我们仔(ting)细(xue)思(zhang)考(jiang)怎么不吸氧通过剩下这几个点

能(xue)想(zhang)到(shuo)用dp来解决这道题。

但是这道题实在是太暴力了，所以我们还是得先暴力一下。

我们依旧先枚举行。然后对列进行dp。

设ver[i]为第i列的元素上下之差的绝对值之和，del[i][j]是第i列与第j列每行的元素之差的绝对值之和，d[i][j]为前i列，选择了j列，这j列中一定有第i列时的最小得分。

简单的画一下ver和del

ver:

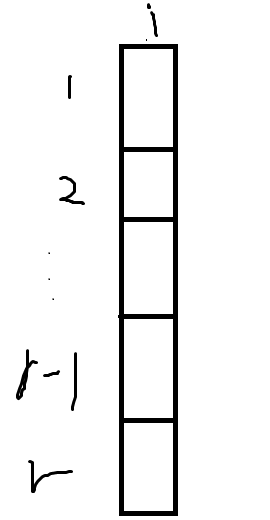
每一个元素减上面那个元素的差的绝对值加起来就是ver

del:

每一行右边减左边的差的绝对值加起来就是del

我们考虑dp[i][j]的转移方程

dp[i][j]可以由dp[i-1][j-1]再选上第i列得到，可以由dp[i-2][j-1]再选第i列得到，可以由dp[i-3][j-1]得到……

所以状态转移方程就是dp[i][j]=min{dp[i][j],dp[i-k][j-1]+ver[i]+del[i-k][i]}(1<=k,i-k>=j-1)

最终答案就是dp[i][c](c<=i<=m)的最小值

#include<bits/stdc++.h>
using namespace std;
int ma[][],n,m,r,c,ans=,ver[],del[][],d[][],ch[];//ch是选择的行
void dp()
{
    memset(d,,sizeof(d));//千万不要memset成0
    memset(ver,,sizeof(ver));
    memset(del,,sizeof(del));
    for(int i=;i<=m;i++)//枚举第i列
     for(int j=;j<=r;j++)//枚举行的编号
      ver[i]+=abs(ma[ch[j]][i]-ma[ch[j-]][i]);
    for(int i=;i<=m;i++)//第i列
     for(int j=i+;j<=m;j++)//第j列
      for(int k=;k<=r;k++)//枚举行（注意循环的顺序）
       del[i][j]+=abs(ma[ch[k]][j]-ma[ch[k]][i]);
    for(int i=;i<=m;i++)
     d[i][]=ver[i];
    for(int i=;i<=m;i++)
     for(int j=;j<=c;j++)
      for(int k=;k<i&&i-k>=j-;k++)
       d[i][j]=min(d[i][j],d[i-k][j-]+ver[i]+del[i-k][i]);

    for(int i=c;i<=m;i++)
     ans=min(ans,d[i][c]);
}
void dfs(int x,int nr)//x，nr的含义与爆搜的含义相同
{

    if(nr==r+)
    {
      dp();
      return;
    }
    if(x>n)return ;
    for(int i=x;i<=n;i++)
        {
            ch[nr]=i;
            dfs(i+,nr+);
        }
}
int main()
{
    scanf("%d%d%d%d",&n,&m,&r,&c);
    for(int i=;i<=n;i++)
     for(int j=;j<=m;j++)
      scanf("%d",&ma[i][j]);
    dfs(,);
    printf("%d",ans);
}