Floyd Cycle Detection

Floyd判圈算法能在O(n)时间复杂度内判断迭代函数或链表中是否有环，并求出环的长度与起点

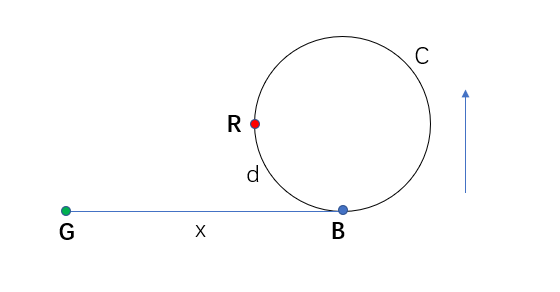
判断环存在

通常采用快慢指针的方式来判断环是否存在

从绿色起点G开始，快指针每次走2步，慢指针每次走1步，当链表未遍历完且快慢指针相遇且时说明链表中存在环

很容易证明：假定链表存在环，那么快慢指针一定会在环内打转，由于存在速度差，则快慢指针一定会相遇

环的长度

若快指针和慢指针在环上的红点R第一次相遇, 则让快指针不动，慢指针继续走并同时从0开始记录步数，则再次相遇时，步数即为环的长度

环的起点

存在环的情况下，假定环的长度为C

同时假定两指针同时从绿点G出发，蓝点B为环的起点，distance(G，B) = x，

，distance(B，R) = d，很容易证明此时慢指针刚好走了C-d步

（不加周期nC，因为慢指针如果在环上走过超过一圈，那么快指针走过超过两圈，则在此之前两指针一定会有一次相遇，这次就不是第一次相遇，详细可自行推倒）

令慢指针走的长度为L，则

L = x + C - d，

2L = nC + x + C - d(n>0, 否则L = 0)

联立可得 nC = x + C - d = L

移项得 x = nC - C + d

如果此时有一个指针S2从绿点出发，和慢指针S1速度相同，则S2与S1相遇时，相遇点即为环的起点

证明：由上式可知，当S2走了x步到达蓝点时，S1正好先走d步到达蓝点，然后再进行非负数个循环，此时S1与S2都在蓝点，得证

例题

141. Linked List Cycle(判断链表是否存在环)

142. Linked List Cycle II(判断链表是否存在环并找出环的起点)

202. Happy Number

// 142题
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        ListNode* slow, *quick, *t;
        t = slow = quick = head;
        while(quick != NULL && quick->next != NULL){
            slow = slow->next;
            quick = quick->next->next;
            if(slow == quick){
                slow = head;
                while(slow != quick){
                    quick = quick->next;
                    slow = slow->next;
                }

                return slow;
            }
        }

        return NULL;
    }
};

// 202题，除了数学方法和基本记忆查询外，还可以采用迭代的方式，这是在迭代函数上进行的
class Solution {
public:
    int digitSquareSum(int n){
        int r = 0, b;
        while(n != 0) {
                b = n % 10;
                n = n / 10;
                r += b * b;
        }
        return r;
    }
    bool isHappy(int n) {

        int slow, fast;

        slow = n;
        fast = n;
        do {
            slow = digitSquareSum(slow);
            fast = digitSquareSum(fast);
            fast = digitSquareSum(fast);
        } while(slow != fast);

        if(slow == 1) return true;
        return false;
    }
};