Codeforces 1173B Nauuo and Chess

题目链接：http://codeforces.com/problemset/problem/1173/B

---

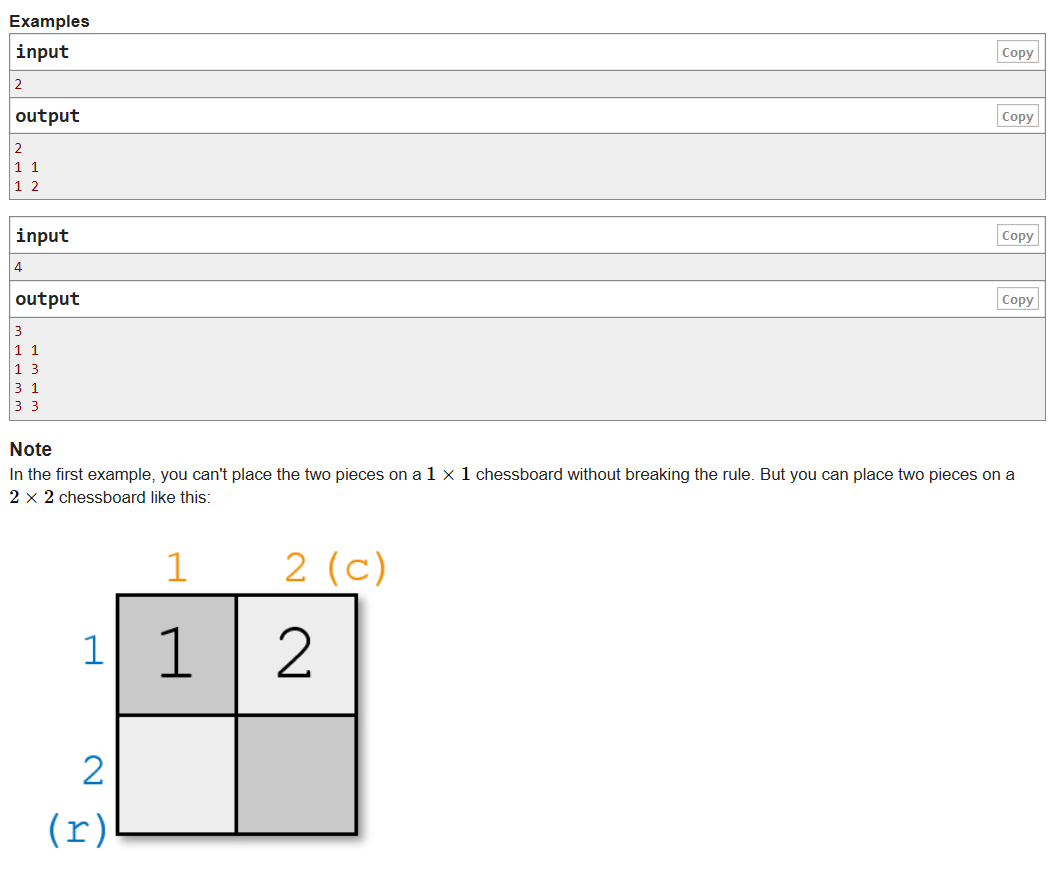
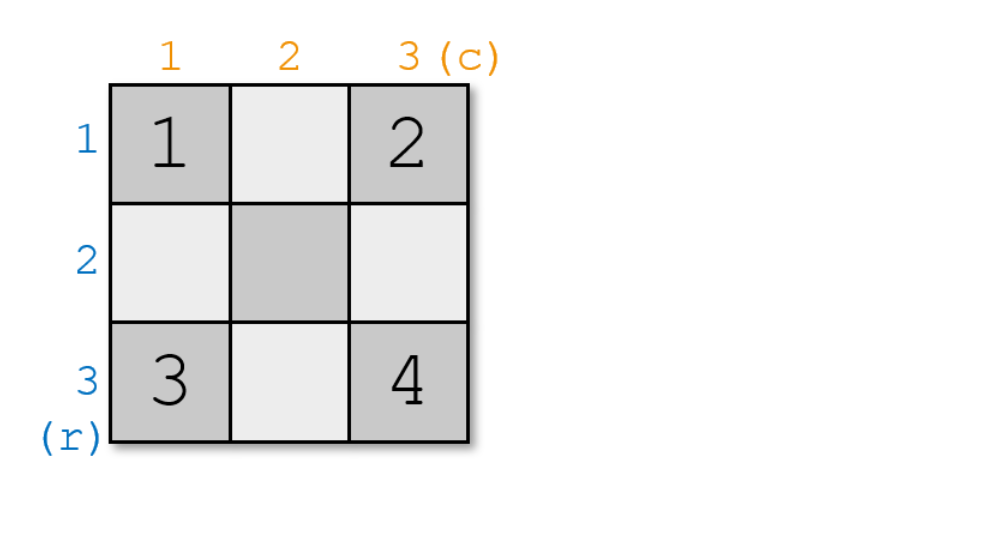
思路参考：https://www.cnblogs.com/blowhail/p/10991237.html

AC代码：

#include<bits/stdc++.h>
using namespace std;
int main()
{
    int n,m;
    cin >> n;
    m = n /  +;
    cout << m << endl;
    for(int i = ;i <= m;i++)
    {
        cout <<  << " " << i << endl;
    }
    for(int i = ;i <= n - m + ;i++)
    {
        cout << i << " " << m << endl;
    }
    return ;
}