剑指offer第二版面试题10：斐波那契数列（JAVA版）

题目：写一个函数，输入n，求斐波那契数列的第n项。斐波那契数列的定义如下：

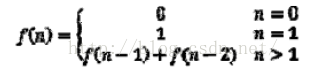
1、效率很低效的解法，挑剔的面试官不会喜欢

使用递归实现:

public class Fibonacci {
    public long getNum(int n){
        if(n<=0){
            return 0;
        }else if(n==1){
            return 1;
        }else{
            return getNum(n-1)+getNum(n-2);
        }
    }
}

我们不难发现在这颗树中有很多的节点是重复的，而且重复的节点数会随着n的增大而急剧增加，这意味着计算量会随着n的增大而急剧增大。事实上，用递归的方法计算的时间复杂度是以n的指数的方式递增的。读者不妨求Fibonacci的第100项试试，感受一下这样的递归会慢到什么程度。

2、面试官期待的适用解法：

其实改进的方法并不复杂，将计算出来的中间项保存起来，减少计算次数

public class Fibonacci2 {
    public long getNum(int n){
        if(n==0){
            return 0;
        }
        if(n==1){
            return 1;
        }
        int temp1=0;//第n-2项的值
        int temp2=1;//第n-1项的值
        int result=0;//保存中间计算出来的结果
        for(int i=2;i<=n;i++){
            result=temp1+temp2;
            temp1=temp2;
            temp2=result;
        }
        return result;
    }
}