CF 286(div 2) B Mr. Kitayuta's Colorful Graph【传递闭包】

解题思路：给出n个点，m条边（即题目中所说的两点之间相连的颜色） 询问任意两点之间由多少种不同的颜色连接

最开始想的时候可以用传递闭包或者并查集来做，可是并查集现在还不会做，就说下用传递闭包来做的这种---

最开始想的时候用传递闭包，可是想到传递闭包只能判断两点是否连通，不能判断连通这两点的颜色是不是一样的，所以当时想再另外用一个数组来放两点之间的颜色，没有写出来----

然后今天去翻了别人的代码，发现把传递闭包的d数组改成三维的就可以解决问题了（因为注意到n,m的值都很小，四重循环再加一个if语句判断一下，不会超时） 即增加的那一维用来储存两点之间的颜色。

B. Mr. Kitayuta's Colorful Graph

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Mr. Kitayuta has just bought an undirected graph consisting of n vertices and m edges. The vertices of the graph are numbered from 1 to n. Each edge, namely edge i, has a color c_i, connecting vertex a_i and b_i.

Mr. Kitayuta wants you to process the following q queries.

In the i-th query, he gives you two integers — u_i and v_i.

Find the number of the colors that satisfy the following condition: the edges of that color connect vertex u_i and vertex v_i directly or indirectly.

Input

The first line of the input contains space-separated two integers — n and m (2 ≤ n ≤ 100, 1 ≤ m ≤ 100), denoting the number of the vertices and the number of the edges, respectively.

The next m lines contain space-separated three integers — a_i, b_i (1 ≤ a_i < b_i ≤ n) and c_i (1 ≤ c_i ≤ m). Note that there can be multiple edges between two vertices. However, there are no multiple edges of the same color between two vertices, that is, if i ≠ j, (a_i, b_i, c_i) ≠ (a_j, b_j, c_j).

The next line contains a integer — q (1 ≤ q ≤ 100), denoting the number of the queries.

Then follows q lines, containing space-separated two integers — u_i and v_i (1 ≤ u_i, v_i ≤ n). It is guaranteed that u_i ≠ v_i.

Output

For each query, print the answer in a separate line.

Sample test(s)

input

4 5 1 2 1 1 2 2 2 3 1 2 3 3 2 4 3 3 1 2 3 4 1 4

output

2 1 0

input

5 7 1 5 1 2 5 1 3 5 1 4 5 1 1 2 2 2 3 2 3 4 2 5 1 5 5 1 2 5 1 5 1 4

output

1 1 1 1 2

Note

Let's consider the first sample.

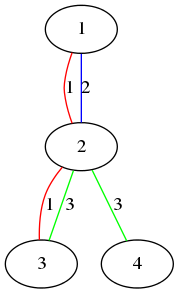The figure above shows the first sample.

• Vertex 1 and vertex 2 are connected by color 1 and 2.
• Vertex 3 and vertex 4 are connected by color 3.
• Vertex 1 and vertex 4 are not connected by any single color.

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define N 105
int d[N][N][N];
int main()
{
	int n,m,q,i,j,k,t,ans,u,v,w,a,b;
	scanf("%d %d",&n,&m);
	for(i=1;i<=m;i++)
	{
		scanf("%d %d %d",&u,&v,&w);
		d[w][u][v]=d[w][v][u]=1;
	}
	for(k=1;k<=n;k++)
		for(t=1;t<=m;t++)
			for(j=1;j<=n;j++)
				if(d[t][i][j]==0)
					for(i=1;i<=n;i++)
				d[t][i][j]=d[t][i][j]||(d[t][i][k]&&d[t][k][j])||d[t][j][i];

	scanf("%d",&q);
	while(q--)
	{
		ans=0;
		scanf("%d %d",&a,&b);
		for(i=1;i<=m;i++)
			if(d[i][a][b])
			ans++;
		printf("%d\n",ans);
	}
}