EC2 Instance扩容EBS卷容量

EC2实例运行一段时间后，由于日志和一些应用程序数据的积累，可能出现之前预留的磁盘容量不够需要扩容的情况。AWS EBS目前还不支持在线扩容，不过可以通过结合snapshot来实现。

如，我的EC2 Instance容量默认的8G不够用了，需要扩容。

1. 创建需要扩容磁盘的snapshot：

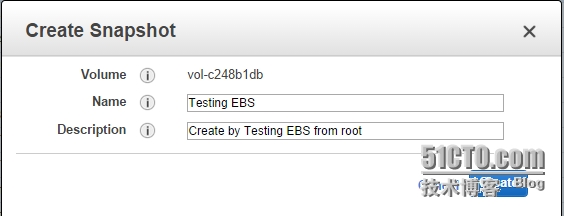
进入aws ec2控制台的Volume管理项中，选中你要扩容的EBS卷，右键选择“create snapshot”

在弹出的对话框中，输入名称和描述信息，待创建完成后记录下snapshot的ID号，下一步有用。

2. 创建一块新Volume，按照自己要扩容的容量

点击“create volume”，根据向导创建一个自己需要的容量Volume，需注意的是Snapshot ID这块，输入的就是上一步创建的“Snapshot的ID”。

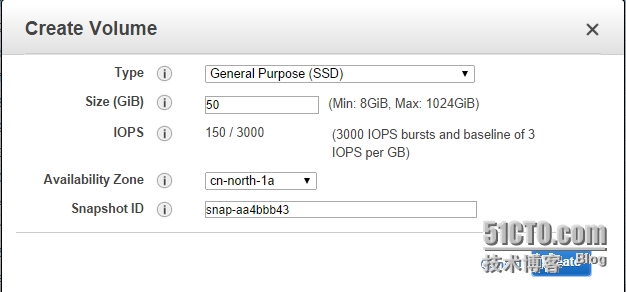
完成后，待Volume状态为“available”时，即完成了Volume的创建。

3. 上新EBS Volume

首先Stop掉EC2实例，选择要扩容的EC2实例，右键选择“Stop”，弹出的对话框中选"yes,stop"

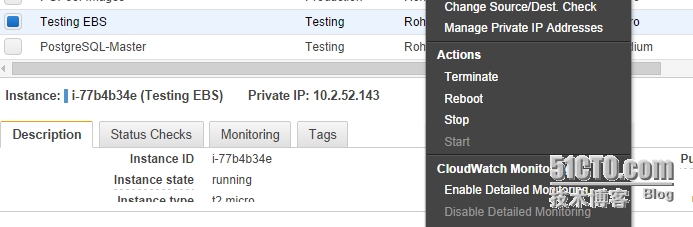
等EC2 Instance状态为“Stopped”时，即可。

然后，分离原有的EBS卷，这块要注意的是记录下这块EBS盘附加的位置,需要将新附加的EBS卷到相同的位置，如下面所示的位置：

选中要分离的EBS Volume，右键，选“Detach Volume”

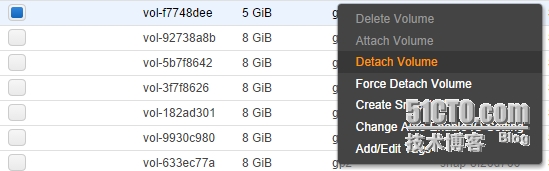
等到状态为“available”时，就可以附加新的EBS Volume了。选中上一步创建的EBS Volume，右键“Attach Volume”

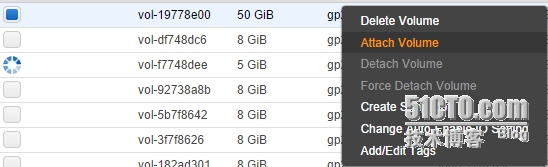
在"Instance"中要输入附加到的“EC2 Instance”的ID，Device就是要附加的位置,这里是“/dev/xvda”:

等状态为“in-use”时，就附加成功了。

最后，启动EC2 Instance 测试,选中“Instance”，右键“start”

连上Instance，查看EBS Volume大小,可以看到/dev/xvda已经是50G了：

root@ip-10-2-32-88:/home/a10070# df -Th
Filesystem     Type      Size  Used Avail Use% Mounted on
/dev/xvda      ext4       50G  1.1G   46G   3% /
udev           devtmpfs   10M     0   10M   0% /dev
tmpfs          tmpfs     200M  4.3M  196M   3% /run
tmpfs          tmpfs     500M     0  500M   0% /dev/shm
tmpfs          tmpfs     500M     0  500M   0% /sys/fs/cgroup
tmpfs          tmpfs     100M     0  100M   0% /run/user
tmpfs          tmpfs     5.0M     0  5.0M   0% /run/lock

注意：

如果连上实例发现磁盘容量df的时候并没有便过来，而fdisk -l时磁盘已经是50G了，那么需要执行命令“resize2fs /dev/xvda”.

如果我们扩容的是另一块非系统的数据盘，其实连实例都不需要停止的。