机器学习之SVM

一、线性分类器：

首先给出一个非常非常简单的分类问题（线性可分），我们要用一条直线，将下图中黑色的点和白色的点分开，很显然，图上的这条直线就是我们要求的直线之一（可以有无数条这样的直线）

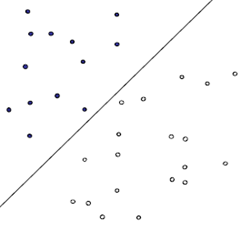
假如说，我们令黑色的点 = -1， 白色的点 =  +1，直线f(x) = w.x + b，这儿的x、w是向量，其实写成这种形式也是等价的f(x) = w1x1 + w2x2 … + wnxn + b, 当向量x的维度=2的时候，f(x) 表示二

维空间中的一条直线， 当x的维度=3的时候，f(x) 表示3维空间中的一个平面，当x的维度=n > 3的时候，表示n维空间中的n-1维超平面。这些都是比较基础的内容，如果不太清楚，可能需要复习一

下微积分、线性代数的内容。

刚刚说了，我们令黑色白色两类的点分别为+1, -1，所以当有一个新的点x需要预测属于哪个分类的时候，我们用sgn(f(x))，就可以预测了，sgn表示符号函数，当f(x) > 0的时候，sgn(f(x)) = +1,

当f(x) < 0的时候sgn(f(x)) = –1。但是，我们怎样才能取得一个最优的划分直线f(x)呢？下图的直线表示几条可能的f(x)

一个很直观的感受是，让这条直线到给定样本中最近的点最远，这句话读起来比较拗口，下面给出几个图，来说明一下： 第一种分法：

第二种分法：

这两种分法哪种更好呢？从直观上来说，就是分割的间隙越大越好，把两个类别的点分得越开越好。就像我们平时判断一个人是男还是女，就是很难出现分错的情况，这就是男、女两个类别之间

的间隙非常的大导致的，让我们可以更准确的进行分类。在SVM中，称为Maximum Marginal，是SVM的一个理论基础之一。选择使得间隙最大的函数作为分割平面是由很多道理的，比如说从概

率的角度上来说，就是使得置信度最小的点置信度最大（听起来很拗口），从实践的角度来说，这样的效果非常好。

上图被红色和蓝色的线圈出来的点就是所谓的支持向量(support vector)。

上图就是一个对之前说的类别中的间隙的一个描述。Classifier Boundary就是f(x)，红色和蓝色的线（plus plane与minus plane）就是support vector所在的面，红色、蓝色线之间的间隙就是我

们要最大化的分类间的间隙。

这里直接给出M的式子：（从高中的解析几何就可以很容易的得到了）

另外支持向量位于wx + b = 1与wx + b = -1的直线上，我们在前面乘上一个该点所属的类别y（还记得吗?y不是+1就是-1），就可以得到支持向量的表达式为：y(wx + b) = 1，这样就可以更简单

的将支持向量表示出来了。当支持向量确定下来的时候，分割函数就确定下来了，两个问题是等价的。得到支持向量，还有一个作用是，让支持向量后方那些点就不用参与计算了。

在这个小节的最后，给出我们要优化求解的表达式：

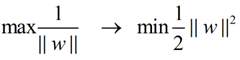
||w||的意思是w的二范数，跟上面的M表达式的分母是一个意思，之前得到，M = 2 / ||w||，最大化这个式子等价于最小化||w||, 另外由于||w||是一个单调函数，我们可以对其加入平方，和前面的系数，

熟悉的同学应该很容易就看出来了，这个式子是为了方便求导。

这个式子有还有一些限制条件，完整的写下来，应该是这样的：（原问题）

s.t的意思是subject to，也就是在后面这个限制条件下的意思，这个词在svm的论文里面非常容易见到。这个其实是一个带约束的二次规划(quadratic programming, QP)问题，是一个凸问题，凸问题

就是指的不会有局部最优解，可以想象一个漏斗，不管我们开始的时候将一个小球放在漏斗的什么位置，这个小球最终一定可以掉出漏斗，也就是得到全局最优解。s.t.后面的限制条件可以看做是一个

凸多面体，我们要做的就是在这个凸多面体中找到最优解。这些问题这里不展开，因为展开的话，一本书也写不完。如果有疑问请看看wikipedia。

二、转化为对偶问题，并优化求解:

这个优化问题可以用拉格朗日乘子法去解，使用了KKT条件的理论，这里直接作出这个式子的拉格朗日目标函数：

求解这个式子的过程需要拉格朗日对偶性的相关知识（另外pluskid也有一篇文章专门讲这个问题），并且有一定的公式推导，如果不感兴趣，可以直接跳到后面用蓝色公式表示的结论，该部分推导主要

参考自plukids的文章。

首先让L关于w，b最小化，分别令L关于w，b的偏导数为0，得到关于原问题的一个表达式

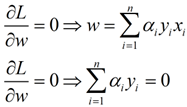
将两式带回L(w,b,a)得到对偶问题的表达式

新问题加上其限制条件是（对偶问题）:

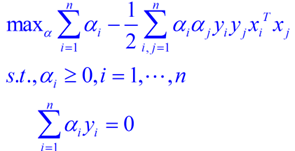
这个就是我们需要最终优化的式子。至此，得到了线性可分问题的优化式子。

求解这个式子，有很多的方法，比如SMO等等，个人认为，求解这样的一个带约束的凸优化问题与得到这个凸优化问题是比较独立的两件事情，所以在这篇文章中准备完全不涉及如何求解这个话题，

如果之后有时间可以补上一篇文章来谈谈:)。

三、线性不可分的情况（软间隔）：

接下来谈谈线性不可分的情况，因为线性可分这种假设实在是太有局限性了：

下图就是一个典型的线性不可分的分类图，我们没有办法用一条直线去将其分成两个区域，每个区域只包含一种颜色的点。

要想在这种情况下的分类器，有两种方式，一种是用曲线去将其完全分开，曲线就是一种非线性的情况，跟之后将谈到的核函数有一定的关系：

另外一种还是用直线，不过不用去保证可分性，就是包容那些分错的情况，不过我们得加入惩罚函数，使 得点分错的情况越合理越好。其实在很多时候，不是在训练的时候分类函数越完美越好，

因为训练函数中有些数据本来就是噪声，可能就是在人工加上分类标签的时候加错了，如果我们在训练（学习）的时候把这些错误的点学习到了，那么模型在下次碰到这些错误情况的时候就难免出

错了（假如老师给你讲课的时候，某个知识点讲错了，你还信以为真了，那么在考试的时候就难免出错）。这种学习的时候学到了“噪声”的过程就是一个过拟合（over-fitting），这在机器学习中是一

个大忌，我们宁愿少学一些内容，也坚决杜绝多学一些错误的知识。还是回到主题，用直线怎么去分割线性不可分的点：

我们可以为分错的点加上一点惩罚，对一个分错的点的惩罚函数就是这个点到其正确位置的距离：

在上图中，蓝色、红色的直线分别为支持向量所在的边界，绿色的线为决策函数，那些紫色的线表示分错的点到其相应的决策面的距离，这样我们可以在原函数上面加上一个惩罚函数，并且带

上其限制条件为：

公式中蓝色的部分为在线性可分问题的基础上加上的惩罚函数部分，当xi在正确一边的时候，ε=0，R为全部的点的数目，C是一个由用户去指定的系数，表示对分错的点加入多少的惩罚，当C很大

的时候，分错的点就会更少，但是过拟合的情况可能会比较严重，当C很小的时候，分错的点可能会很多，不过可能由此得到的模型也会不太正确，所以如何选择C是有很多学问的，不过在大部分情

况下就是通过经验尝试得到的。

接下来就是同样的，求解一个拉格朗日对偶问题，得到一个原问题的对偶问题的表达式：

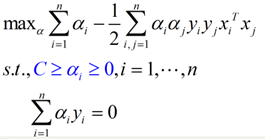
蓝色的部分是与线性可分的对偶问题表达式的不同之处。在线性不可分情况下得到的对偶问题，不同的地方就是α的范围从[0, +∞)，变为了[0, C]，增加的惩罚ε没有为对偶问题增加什么复杂度。

四、核函数：

刚刚在谈不可分的情况下，提了一句，如果使用某些非线性的方法，可以得到将两个分类完美划分的曲线，比如接下来将要说的核函数。

    我们可以让空间从原本的线性空间变成一个更高维的空间，在这个高维的线性空间下，再用一个超平面进行划分。这儿举个例子，来理解一下如何利用空间的维度变得更高来帮助我们分类的

下图是一个典型的线性不可分的情况

但是当我们把这两个类似于椭圆形的点映射到一个高维空间后，映射函数为：

    用这个函数可以将上图的平面中的点映射到一个三维空间（z1,z2,z3)，并且对映射后的坐标加以旋转之后就可以得到一个线性可分的点集了。

用另外一个哲学例子来说：世界上本来没有两个完全一样的物体，对于所有的两个物体，我们可以通过增加维度来让他们最终有所区别，比如说两本书，从(颜色，内容)两个维度来说，

可能是一样的，我们可以加上 作者 这个维度，是在不行我们还可以加入 页码，可以加入 拥有者，可以加入 购买地点，可以加入 笔记内容等等。当维度增加到无限维的时候，一定可以让任

意的两个物体可分了。

回忆刚刚得到的对偶问题表达式：

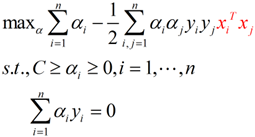
我们可以将红色这个部分进行改造，令：     这个式子所做的事情就是将线性的空间映射到高维的空间,k(x, xj)有很多种，下面是比较典型的两种：

上面这个核称为多项式核，下面这个核称为高斯核，高斯核甚至是将原始空间映射为无穷维空间，另外核函数有一些比较好的性质，比如说不会比线性条件下增加多少额外的计算量，等等，

这里也不再深入。一般对于一个问题，不同的核函数可能会带来不同的结果，一般是需要尝试来得到的。

五、参考资料

（1）周志华的西瓜书。不过省略了很多原理和中间的步骤，不太好懂。

（2）博客：SVM的三层境界，推导和原理写的最透的一篇博客，https://blog.csdn.net/macyang/article/details/38782399

本文转自http://www.cnblogs.com/LeftNotEasy/archive/2011/05/02/basic-of-svm.html