神经网络优化篇：详解神经网络的权重初始化（Weight Initialization for Deep NetworksVanishing / Exploding gradients）

神经网络的权重初始化

这是一个神经单元初始化地例子，然后再演变到整个深度网络。

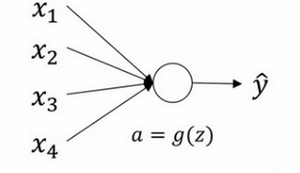
来看看只有一个神经元的情况，然后才是深度网络。

单个神经元可能有4个输入特征，从\(x_{1}\)到\(x_{4}\)，经过\(a=g(z)\)处理，最终得到\(\hat{y}\)，稍后讲深度网络时，这些输入表示为\(a^{[l]}\)，暂时用\(x\)表示。

\(z = w_{1}x_{1} + w_{2}x_{2} + \ldots +w_{n}x_{n}\)，\(b=0\)，暂时忽略\(b\)，为了预防\(z\)值过大或过小，可以看到\(n\)越大，希望\(w_{i}\)越小，因为\(z\)是\(w_{i}x_{i}\)的和，如果把很多此类项相加，希望每项值更小，最合理的方法就是设置\(w_{i}=\frac{1}{n}\)，\(n\)表示神经元的输入特征数量，实际上，要做的就是设置某层权重矩阵\(w^{[l]} = np.random.randn( \text{shape})*\text{np.}\text{sqrt}(\frac{1}{n^{[l-1]}})\)，\(n^{[l - 1]}\)就是喂给第\(l\)层神经单元的数量（即第\(l-1\)层神经元数量）。

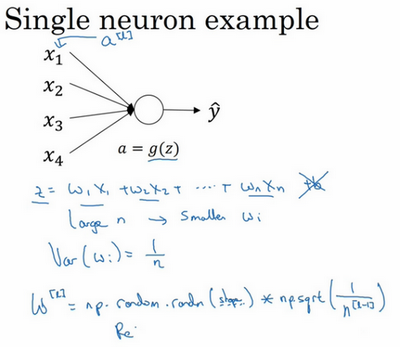
结果，如果是用的是Relu激活函数，而不是\(\frac{1}{n}\)，方差设置为\(\frac{2}{n}\)，效果会更好。常常发现，初始化时，尤其是使用Relu激活函数时，\(g^{[l]}(z) =Relu(z)\),它取决于对随机变量的熟悉程度，这是高斯随机变量，然后乘以它的平方根，也就是引用这个方差\(\frac{2}{n}\)。这里，用的是\(n^{[l - 1]}\)，因为本例中，逻辑回归的特征是不变的。但一般情况下\(l\)层上的每个神经元都有\(n^{[l - 1]}\)个输入。如果激活函数的输入特征被零均值和标准方差化，方差是1，\(z\)也会调整到相似范围，这就没解决问题（梯度消失和爆炸问题）。但它确实降低了梯度消失和爆炸问题，因为它给权重矩阵\(w\)设置了合理值，也知道，它不能比1大很多，也不能比1小很多，所以梯度没有爆炸或消失过快。

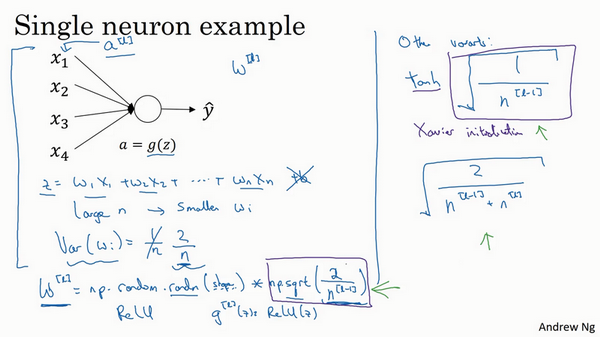
提到了其它变体函数，刚刚提到的函数是Relu激活函数，一篇由Herd等人撰写的论文曾介绍过。对于几个其它变体函数，如tanh激活函数，有篇论文提到，常量1比常量2的效率更高，对于tanh函数来说，它是\(\sqrt{\frac{1}{n^{[l-1]}}}\)，这里平方根的作用与这个公式作用相同(\(\text{np.}\text{sqrt}(\frac{1}{n^{[l-1]}})\))，它适用于tanh激活函数，被称为Xavier初始化。Yoshua Bengio和他的同事还提出另一种方法，可能在一些论文中看到过，它们使用的是公式\(\sqrt{\frac{2}{n^{[l-1]} + n^{\left[l\right]}}}\)。其它理论已对此证明，但如果想用Relu激活函数，也就是最常用的激活函数，会用这个公式\(\text{np.}\text{sqrt}(\frac{2}{n^{[l-1]}})\)，如果使用tanh函数，可以用公式\(\sqrt{\frac{1}{n^{[l-1]}}}\)，有些作者也会使用这个函数。

实际上，认为所有这些公式只是给一个起点，它们给出初始化权重矩阵的方差的默认值，如果想添加方差，方差参数则是另一个需要调整的超级参数，可以给公式\(\text{np.}\text{sqrt}(\frac{2}{n^{[l-1]}})\)添加一个乘数参数，调优作为超级参数激增一份子的乘子参数。有时调优该超级参数效果一般，这并不是想调优的首要超级参数，但发现调优过程中产生的问题，虽然调优该参数能起到一定作用，但考虑到相比调优，其它超级参数的重要性，通常把它的优先级放得比较低。

希望现在对梯度消失或爆炸问题以及如何为权重初始化合理值已经有了一个直观认识，希望设置的权重矩阵既不会增长过快，也不会太快下降到0，从而训练出一个权重或梯度不会增长或消失过快的深度网络。在训练深度网络时，这也是一个加快训练速度的技巧。