2017年第八届 蓝桥杯C组 C/C++决赛题解

蓝桥杯历年国赛真题汇总：Here

1.哥德巴赫分解

哥德巴赫猜想认为：不小于4的偶数都可以表示为两个素数的和。

你不需要去证明这个定理，但可以通过计算机对有限数量的偶数进行分解，验证是否可行。

实际上，一般一个偶数会有多种不同的分解方案，我们关心包含较小素数的那个方案。

对于给定数值范围，我们想知道这些包含较小素数方案中最大的素数是多少。

比如，100以内，这个数是19，它由98的分解贡献。

你需要求的是10000以内，这个数是多少？

答案：173

const int N = 10000;
vector<int>prime;
bool vis[10010];
int ans;
void check(int n) {
    for (int i = 0; i < prime.size(); ++i) {
        int r = n - prime[i];
        if (vis[r]) {
            ans = max(ans, prime[i]);
            return ;
        }
    }
}
void solve() {
    memset(vis, true, sizeof(vis));
    for (int i = 2; i < N; ++i)
        if (vis[i])for (int j = i + i; j < N; j += i)vis[j] = false;
    for (int i = 2; i < N; ++i)if (vis[i])prime.push_back(i);
    for (int i = 4; i < 10000; i += 2)check(i);
    cout << ans << "\n";
}

2.数字划分

w星球的长老交给小明一个任务：

1,2,3...16 这16个数字分为两组。

要求：

这两组数字的和相同，

并且，两组数字的平方和也相同，

并且，两组数字的立方和也相同。

请你利用计算机的强大搜索能力解决这个问题。

并提交1所在的那个分组的所有数字。

这些数字要从小到大排列，两个数字间用一个空格分开。

即类似：1 4 5 8 ... 这样的答案。

注意，只提交这一组数字，不要填写任何多余的内容。

---

笨笨有话说：

只要一个组的成员确定了，另一个组的成员也就确定了。枚举一个组的成员就可以了。

凭直觉，两个组的成员数目不会差太多吧。

歪歪有话说：

既然求 1 所在的那个组，那只要枚举剩余的成员就可以了。

貌似都是8个成员的可能性很大啊。

答案：1 4 6 7 10 11 13 16

爆搜

bool vis[17];
void dfs(int pos, int cnt) {
    if (cnt == 8) {
        int sum1 = 0, sum2 = 0, sum11 = 0, sum22 = 0;
        for (int i = 1; i <= 16; ++i) {
            if (!vis[i])sum1 += i * i, sum2 += i * i * i;
            else sum11 += i * i, sum22 += i * i * i;
        }
        if (sum1 == sum11 and sum2 == sum22) {
            for (int i = 1; i <= 16; ++i)if (!vis[i]) cout << i << " " ;
            cout << "\n"; return; // 找到一组就直接推出即可
        }
        return ;
    }
    for (int i = pos + 1; i <= 16; ++i) {
        if (!vis[i])continue;
        vis[i] = false;
        dfs(i, cnt + 1);
        vis[i] = true;
    }
}

3.表达式计算

虽然我们学了许久的程序设计，但对于简单的四则混合运算式，如果让我们完全白手起家地编程来解析，还是有点棘手。

这里，我们简化一下问题，假设只有加法和乘法，并且没有括号来改变优先级。

再假设参加运算的都是正整数。

在这么多的限制条件下，表达式的解析似乎简单了许多。

下面的代码解决了这个问题。请仔细阅读源码，并填写划线部分缺少的代码。

#include <stdio.h>

int f3(const char* s, int begin, int end) {
    int sum = 0;
    int i;
    for (i = begin; i < end; i++) {
        if (s[i] == ' ') continue;
        sum = sum * 10 + (s[i] - '0');
    }
    return sum;
}

int f2(const char* s, int begin, int end) {
    int p = begin;
    int pro = 1;
    while (1) {
        int p0 = p;
        while (p != end && s[p] != '*') p++;
        pro *= _______________________________;  //填空
        if (p == end) break;
        p++;
    }
    printf("f2: pro=%d\n", pro);
    return pro;
}

int f(const char* s) {
    int p = 0;
    int sum = 0;
    while (1) {
        int p0 = p;
        while (s[p] != 0 && s[p] != '+') p++;
        sum += f2(s, p0, p);
        if (s[p] == 0) break;
        p++;
    }
    return sum;
}

int main() {
    int x = f("12+18+5*4*3+10");
    printf("%d\n", x); // 100
    return 0;
}

注意：只填写划线处缺少的内容，不要填写已有的代码或符号，也不要填写任何解释说明文字等。

答案：f3(s, p0, p)

仔细阅读代码即可

4.小数第n位

我们知道，整数做除法时，有时得到有限小数，有时得到无限循环小数。

如果我们把有限小数的末尾加上无限多个0，它们就有了统一的形式。

本题的任务是：在上面的约定下，求整数除法小数点后的第n位开始的3位数。

输入：

一行三个整数：a b n，用空格分开。a是被除数，b是除数，n是所求的小数后位置（0<a,b,n<1000000000）

输出：

一行3位数字，表示：a除以b，小数后第n位开始的3位数字。

比如：

输入：

1 8 1

程序应该输出：

125

再比如：

输入：

1 8 3

程序应该输出：

500

再比如：

输入：

282866 999000 6

程序应该输出：

914

提交时，注意选择所期望的编译器类型。

---

笨笨有话说：

这个除法小学就会算啊，模拟手算除法的过程就可以了吧。

只是数有点大啊....

管它呢，能算多远算多远....

歪歪有话说：

如果我能确定循环节从哪里开始到哪里结束，再大的数不过就是与它取模的余数等价啊

【思路】

模拟除法。
    13 / 7 = 1.85714285...

这里求小数部分，所有取模忽略掉整数部分
13 / 7 -> 6 / 7

第一位：（小数点后第几位，以下同）6 * 10 / 7 = 8；
得到第一位后的余数：6 * 10 % 7 = 4

那么第二位：4 * 10 / 7 = 5
得到第二位后的余数：4 * 10 % 7 = 5

第三位：5 * 10 / 7 = 7

依此类推

void solve() {
    ll a, b, n;
    cin >> a >> b >> n;
    a %= b;
    while (n > 10) {
        a *= 1E10; a %= b; n -= 10;
    }
    for (int i = 0; i < n + 2; ++i) {
        a *= 10;
        if (i >= n - 1)cout << a / b;
        a %= b;
    }
}

5.分考场

n个人参加某项特殊考试。

为了公平，要求任何两个认识的人不能分在同一个考场。

求最少需要分几个考场才能满足条件。

输入格式：

第一行，一个整数n(1<n<100)，表示参加考试的人数。

第二行，一个整数m，表示接下来有m行数据

以下m行每行的格式为：两个整数a，b，用空格分开 (1<=a,b<=n) 表示第a个人与第b个人认识（编号从1开始）。

输出格式：

一行一个整数，表示最少分几个考场。

例如：

输入：

5
8
1 2
1 3
1 4
2 3
2 4
2 5
3 4
4 5

程序应该输出：

4

再比如：

输入：

5
10
1 2
1 3
1 4
1 5
2 3
2 4
2 5
3 4
3 5
4 5

则程序应该输出：

5

资源约定：

峰值内存消耗 < 256M

CPU消耗 < 1000ms

【思路】

一开始以为是并查集之类的连通图大小的问题，写了一发结果只通过 30% 的数据，重新审题发现其实就是图的着色问题：给定顶点数和边，求至少需要多少种颜色对图进行涂色能是相邻顶点颜色不同。

const int N = 110, inf = 0x3f3f3f3f;
int e[N][N];
int vis[N][N]; // vis[i][j] = t表示第i个考场里面第j个人是t
int cnt[N]; // 记录每个考场种的学生数量（对应的vis）
int ans = inf, n, m;
void dfs(int id, int num) {// id表示第id个学生，num表示当前考场编号
	if (num >= ans)return;
	if (id > n) {  // 学生已经安排完了
		ans = min(ans, num);// 更新当前最优解（不要用min可能超时）
		return;
	}
	for (int i = 1; i <= num; ++i) {// 先看之前分配为的考场里面能不能进去
		int rnd = 0;// 表示id学生与第i个考场里面的人不认识的数量
		for (int j = 1; j <= cnt[i]; ++j) // cnt[i]表示第i个考场里面的人数
			if (e[id][vis[i][j]] == 0)rnd ++;
		if (rnd == cnt[i]) { // 如果都不认识
			vis[i][++cnt[i]] = id;
			dfs(id + 1, num);
			cnt[i]--;// 回溯
		}
	}
	// 现有考场都不行，就要增加考场
	vis[num + 1][++cnt[num + 1]] = id;
	dfs(id + 1, num + 1);
	--cnt[num + 1]; // 回溯
}
void solve() {
	cin >> n >> m;
	while (m--) {
		int u, v;
		cin >> u >> v;
		e[u][v] = e[v][u] = 1;
	}
	dfs(1, 0);
	cout << ans << "\n";
}

6.合根植物

w星球的一个种植园，被分成 m * n 个小格子（东西方向m行，南北方向n列）。每个格子里种了一株合根植物。

这种植物有个特点，它的根可能会沿着南北或东西方向伸展，从而与另一个格子的植物合成为一体。

如果我们告诉你哪些小格子间出现了连根现象，你能说出这个园中一共有多少株合根植物吗？

输入格式：

第一行，两个整数m，n，用空格分开，表示格子的行数、列数（1<m,n<1000）。

接下来一行，一个整数k，表示下面还有k行数据(0<k<100000)

接下来k行，第行两个整数a，b，表示编号为a的小格子和编号为b的小格子合根了。

格子的编号一行一行，从上到下，从左到右编号。

比如：5 * 4 的小格子，编号：

1  2  3  4
5  6  7  8
9  10 11 12
13 14 15 16
17 18 19 20

样例输入：

5 4
16
2 3
1 5
5 9
4 8
7 8
9 10
10 11
11 12
10 14
12 16
14 18
17 18
15 19
19 20
9 13
13 17

样例输出：

5

其合根情况参考图[p1.png]

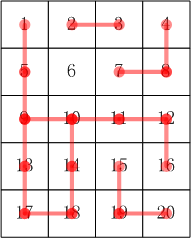
资源约定：

峰值内存消耗 < 256M

CPU消耗 < 2000ms

待补