神经网络基础篇：详解logistic 损失函数（Explanation of logistic regression cost function）

详解 logistic 损失函数

在本篇博客中，将给出一个简洁的证明来说明逻辑回归的损失函数为什么是这种形式。

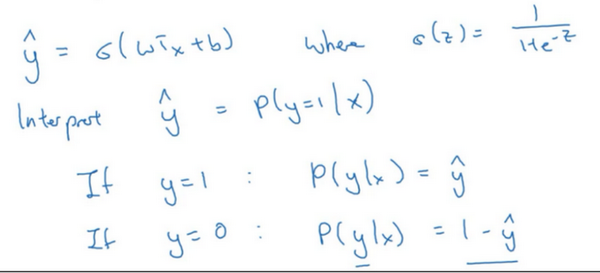
回想一下，在逻辑回归中，需要预测的结果\(\hat{y}\),可以表示为\(\hat{y}=\sigma(w^{T}x+b)\)，\(\sigma\)是熟悉的\(S\)型函数 \(\sigma(z)=\sigma(w^{T}x+b)=\frac{1}{1+e^{-z}}\) 。约定 \(\hat{y}=p(y=1|x)\) ，即算法的输出\(\hat{y}\) 是给定训练样本 \(x\) 条件下 \(y\) 等于1的概率。换句话说，如果\(y=1\)，在给定训练样本 \(x\) 条件下\(y=\hat{y}\)；反过来说，如果\(y=0\)，在给定训练样本\(x\)条件下 \(y\) 等于1减去\(\hat{y}(y=1-\hat{y})\)，因此，如果 \(\hat{y}\) 代表 \(y=1\) 的概率，那么\(1-\hat{y}\)就是 \(y=0\)的概率。接下来，就来分析这两个条件概率公式。

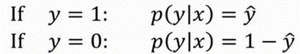
这两个条件概率公式定义形式为 \(p(y|x)\)并且代表了 \(y=0\) 或者 \(y=1\) 这两种情况，可以将这两个公式合并成一个公式。需要指出的是讨论的是二分类问题的损失函数，因此，\(y\)的取值只能是0或者1。上述的两个条件概率公式可以合并成如下公式：

\(p(y|x)={\hat{y}}^{y}{(1-\hat{y})}^{(1-y)}\)

接下来会解释为什么可以合并成这种形式的表达式：\((1-\hat{y})\)的\((1-y)\)次方这行表达式包含了上面的两个条件概率公式，现在来解释一下为什么。

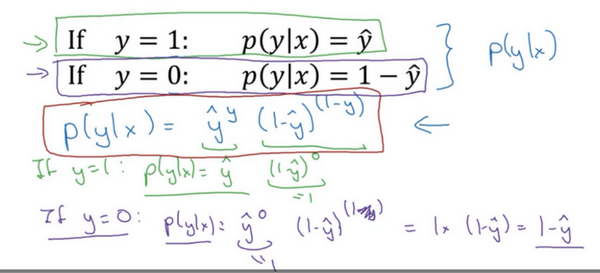
第一种情况，假设 \(y=1\)，由于\(y=1\)，那么\({(\hat{y})}^{y}=\hat{y}\)，因为 \(\hat{y}\)的1次方等于\(\hat{y}\)，\(1-{(1-\hat{y})}^{(1-y)}\)的指数项\((1-y)\)等于0，由于任何数的0次方都是1，\(\hat{y}\)乘以1等于\(\hat{y}\)。因此当\(y=1\)时 \(p(y|x)=\hat{y}\)（图中绿色部分）。

第二种情况，当 \(y=0\) 时 \(p(y|x)\) 等于多少呢?

假设\(y=0\)，\(\hat{y}\)的\(y\)次方就是 $$\hat{y}$$ 的0次方，任何数的0次方都等于1，因此 \(p(y|x)=1×{(1-\hat{y})}^{1-y}\) ，前面假设 \(y=0\) 因此\((1-y)\)就等于1，因此 \(p(y|x)=1×(1-\hat{y})\)。因此在这里当\(y=0\)时，\(p(y|x)=1-\hat{y}\)。这就是这个公式(第二个公式，图中紫色字体部分)的结果。

因此，刚才的推导表明 \(p(y|x)={\hat{y}}^{(y)}{(1-\hat{y})}^{(1-y)}\)，就是 \(p(y|x)\) 的完整定义。由于 log 函数是严格单调递增的函数，最大化 \(log(p(y|x))\) 等价于最大化 \(p(y|x)\) 并且地计算 \(p(y|x)\) 的 log对数，就是计算 \(log({\hat{y}}^{(y)}{(1-\hat{y})}^{(1-y)})\) (其实就是将 \(p(y|x)\) 代入)，通过对数函数化简为：

\(ylog\hat{y}+(1-y)log(1-\hat{y})\)

而这就是前面提到的损失函数的负数 \((-L(\hat{y},y))\) ，前面有一个负号的原因是当训练学习算法时需要算法输出值的概率是最大的（以最大的概率预测这个值），然而在逻辑回归中需要最小化损失函数，因此最小化损失函数与最大化条件概率的对数 \(log(p(y|x))\) 关联起来了，因此这就是单个训练样本的损失函数表达式。

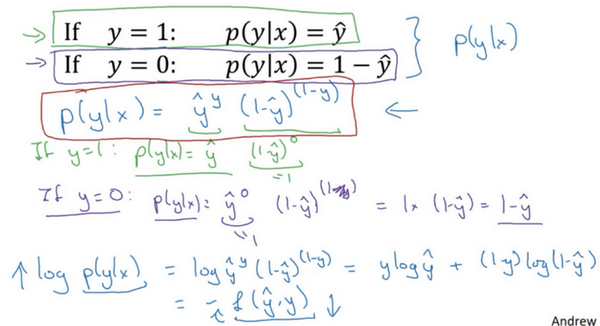
在 \(m\)个训练样本的整个训练集中又该如何表示呢。

整个训练集中标签的概率，更正式地来写一下。假设所有的训练样本服从同一分布且相互独立，也即独立同分布的，所有这些样本的联合概率就是每个样本概率的乘积:

\(P\left(\text{labels in training set} \right) = \prod_{i =1}^{m}{P(y^{(i)}|x^{(i)})}\)。

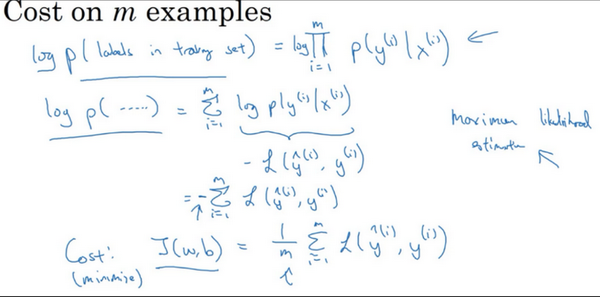
如果想做最大似然估计，需要寻找一组参数，使得给定样本的观测值概率最大，但令这个概率最大化等价于令其对数最大化，在等式两边取对数：

\(logp\left( \text{labels in training set} \right) = log\prod_{i =1}^{m}{P(y^{(i)}|x^{(i)})} = \sum_{i = 1}^{m}{logP(y^{(i)}|x^{(i)})} = \sum_{i =1}^{m}{- L(\hat y^{(i)},y^{(i)})}\)

在统计学里面，有一个方法叫做最大似然估计，即求出一组参数，使这个式子取最大值，也就是说，使得这个式子取最大值，\(\sum_{i= 1}^{m}{- L(\hat y^{(i)},y^{(i)})}\)，可以将负号移到求和符号的外面，\(- \sum_{i =1}^{m}{L(\hat y^{(i)},y^{(i)})}\)，这样就推导出了前面给出的logistic回归的成本函数\(J(w,b)= \sum_{i = 1}^{m}{L(\hat y^{(i)},y^{\hat( i)})}\)。

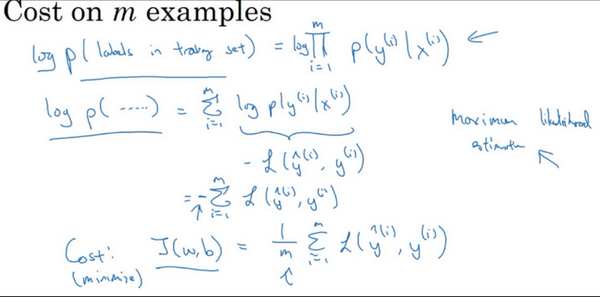
由于训练模型时，目标是让成本函数最小化，所以不是直接用最大似然概率，要去掉这里的负号，最后为了方便，可以对成本函数进行适当的缩放，就在前面加一个额外的常数因子\(\frac{1}{m}\)，即:\(J(w,b)= \frac{1}{m}\sum_{i = 1}^{m}{L(\hat y^{(i)},y^{(i)})}\)。

总结一下，为了最小化成本函数\(J(w,b)\)，从logistic回归模型的最大似然估计的角度出发，假设训练集中的样本都是独立同分布的条件下。